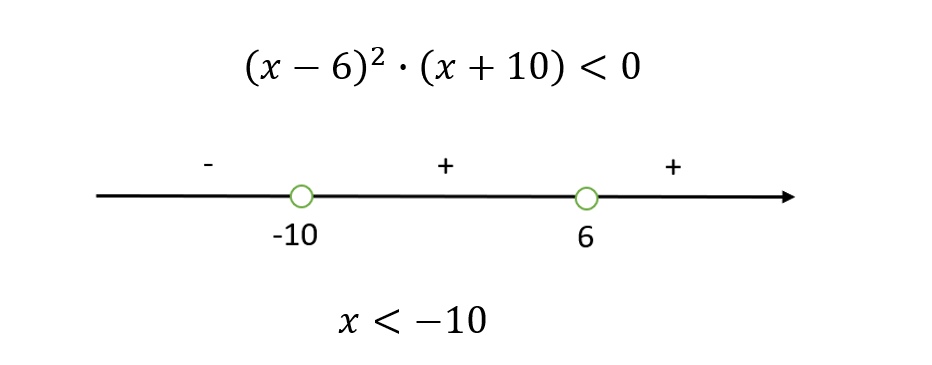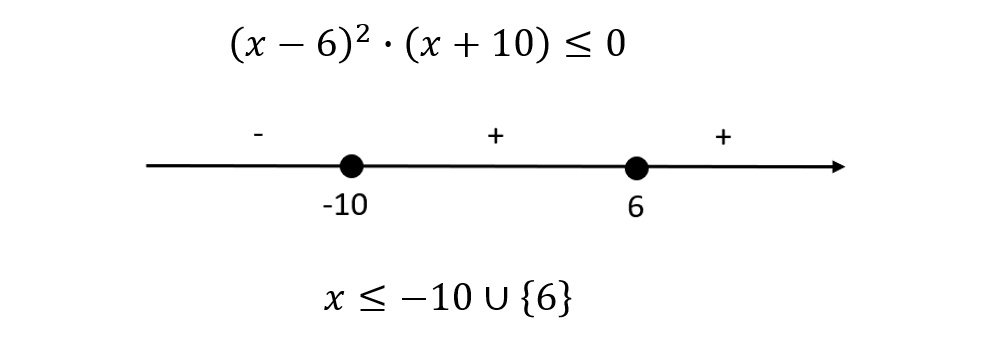- Задание 15. Неравенства. ЕГЭ 2024 по математике профильного уровня
- Что нужно знать, чтобы решить задание 15:
- Задачи для практики
- Задача 1
- Задача 2
- Задача 3
- Задача 4
- Задача 5
- Задача 6
- Задача 7
- Задача 8
- Задача 9
- Задача 10
- Задача 11
- Задача 12
- Задача 13
- Задача 14
- Задача 15
- Задача 16
- Задача 17
- Задача 18
- Задача 19
- Метод интервалов
- Пример 1
- Пример 2
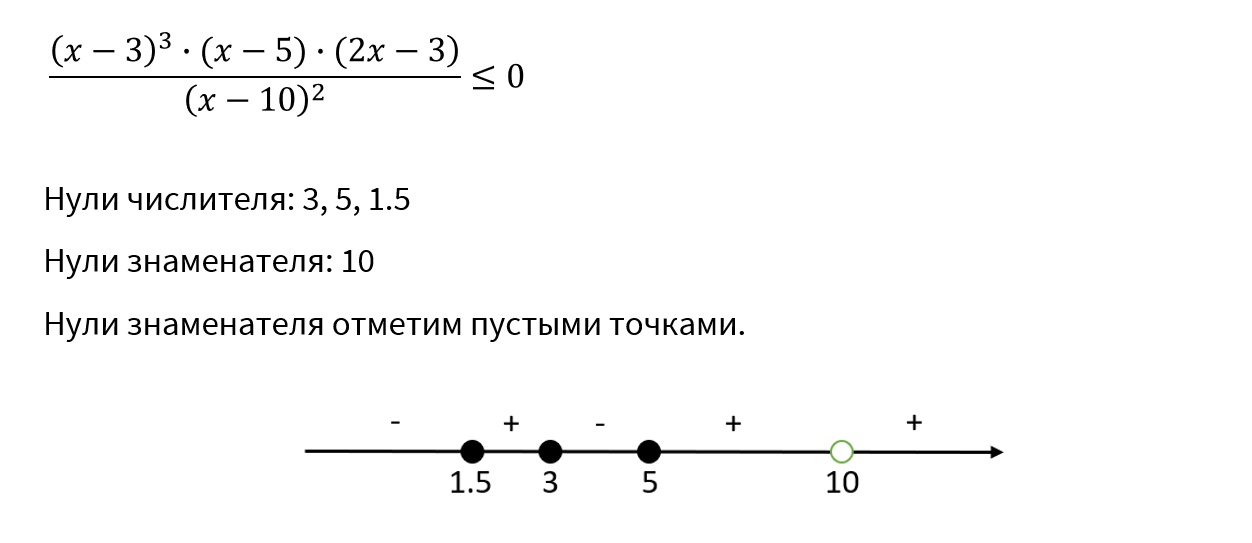
- Пример 3
- Пример неравенства №15
Задание 15. Неравенства. ЕГЭ 2024 по математике профильного уровня
Средний процент выполнения: 2.7%
Ответом к заданию 15 по математике (профильной) может быть развернутый ответ (полная запись решения с обоснованием выполненных действий).
Что нужно знать, чтобы решить задание 15:
Необходимо свести сложное неравенство к простейшему. Для этого нужно знать метод замены показательных и тригонометрических функций, помня про ограничения. Знать метод интервалов и метод рационализации для логарифмических, показательных и содержащих модуль неравенств.
Задачи для практики
Задача 1
Решите неравенство: $log_7^2(9-x^2)-10log_7(9-x^2)+21⩾ 0$.
Решение
$log_7^2(9 — x^2) — 10 log_7(9 — x^2) + 21 ≥ 0$.
Обозначим $log_7 (9 — x^2) = t$. Неравенство примет вид: $t^2 — 10t + 21 ≥ 0, (t — 3)(t — 7) ≥ 0$, отсюда $t ≤ 3, t ≥ 7$.
${tablelog_7 (9 — x^2) ≤ 3; 9 — x^2 > 0;$ или ${tablelog_7 (9 — x^2) ≥ 7; 9 — x^2 > 0;$ ${table9-x^2 ≤ 7^3; x^2 < 9;$или ${table9-x^2 ≥ 7^7; x^2 < 9;$
${tablex^2 ≥ 9 — 7^3; x^2 < 9;$ или ${tablex^2 ≤ 9-7^7; x^2 < 9;$, система решений не имеет ${tablex^2 ≥ 9-7^3; -3 < x < 3;$
Отсюда $x ∈ (-3; 3)$.
Задача 2
Решите неравенство: ${4^{x}+16} / {4^x-16}+{4^x-16} / {4^x+16}⩾{4⋅ 4^{x+1}+480} / {16^x-256}$.
Решение
${4^x+16}/{4^x — 16} + {4^x — 16}/{4^x +16} ≥ {4·4^{x+1} + 480}/{16^x — 256}$;
${(4^x +16)^2 + (4^x — 16)^2}/{(4^x — 16)(4^x +16)} ≥ {4·4^{x+1} + 480}/{(4^x — 16)(4^x + 16)}$,
${4^{2x} +32 · 4^x + 256 + 4^{2x} — 32 · 4^x + 256-480-16· 4^x}/{(4^x — 16)(4^x +16)} ≥ 0$,
${4^{2x} — 8 · 4^x + 16}/{(4^x — 16)(4^x +16)} ≥ 0$,
${(4^x — 4)^2}/{(4^x — 16)(4^x +16)} ≥ 0$.
Обозначим $4^x = t, t > 0$ и найдём решения неравенства ${(t — 4)^2}/{(t — 16)(t +16)} ≥ 0$.
Числитель положительное число, либо равное нулю при $t = 4$, то есть $4^x = 4, x = 1$.
Знаменатель — положительное число при $t < -16$ или $t > 16$.
А так как $t > 0$, то $t > 16$, то есть $4^x > 16, x > 2$.
Итак, $x ∈ {1}∪(2; +∞)$.
Задача 3
Решите неравенство: ${6} / {log_4x}-{log_4x} / {log_4{x} / {256}}⩾{15} / {log_4x^4-log_4^2x}$.
Решение
${6}/{log_4x} — {log_4x}/{log_4{x}/{256}} ≥ {15}/{log_4x^4-log_4^2x}$
ОДЗ: $x > 0, x ≠ 256, x ≠ 1$.
${6}/{log_4x} — {log_4x}/{log_4x-4} ≥ {15}/{4log_4x-log_4^2x}$;
${6}/{log_4x} — {log_4x}/{log_4x-4} ≥ {15}/{log_4x(4-log_4x)}$.
${6(log_4x-4)-log_4^2x}/{log_4x(log_4x-4)} ≥ {-15}/{log_4x(log_4x-4)}$.
${6log_4x-24-log_4^2x+15}/{log_4x(log_4x-4)} ≥ 0$
${log_4^2x-6log_4x+9}/{log_4x(log_4x-4)}≤ 0$
${(log_4x-3)^2}/{log_4x(log_4x-4)}≤ 0$
Обозначим $log_4 x = t$. Неравенство примет вид: ${(t — 3)^2}/{t(t — 4)} ≤ 0$.
Решим это неравенство методом интервалов.
Итак, $0 < log_4x < 4, 1 < x <256$.
Задача 4
Решите неравенство ${50⋅ 3^x-100+50⋅ 3^{-x}} / {3^x+3^{-x}+2}-{20+20⋅ 3^x} / {3^x+1}⩽ {3^{x+1}⋅ 5-15} / {3^x+1}$.
Решение
${50·3^x — 100 + 50 · 3^{-x}}/{3^x + 3^{-x} + 2} — {20 + 20 · 3^x}/{3^x + 1} ≤ {5· 3^{x+1} — 15}/{3^x + 1}$.
Выполним преобразования, обозначив $3^x = t, t > 0$.
${50t +{50}/{t} — 100}/{t + {1}/{t} + 2} — {20 + 20t}/{t + 1} ≤ {15t — 15}/{t + 1}$,
${50(t^2 — 2t + 1)}/{t^2 + 2t + 1} — {20(1 + t)}/{t + 1} ≤ {15(t — 1)}/{t + 1}$
Так как $t > 0$, то ${t^2 + 2t + 1}>0$ и ${t + 1}>0$
Значит мы можем привести неравенство к следующему виду
$50(t^2 — 2t + 1) — 20(t + 1)^2 — 15(t — 1)(t + 1) ≤ 0$,
$50t^2 — 100t + 50 — 20t^2 — 40t — 20 — 15t^2 + 15 ≤ 0$,
$15t^2 — 140t + 45 ≤ 0, 3t^2 — 28t + 9 ≤ 0$.
$3t^2 — 28t + 9 = 0, D = 28^2 — 27 · 4 = 676 = 26^2$.
$t_1 ={1}/{3}, t_2 = 9$.
Решением неравенства $3t^2 — 28t + 9 ≤ 0$ будет $t ∈ [{1}/{3}; 9]$.
Переходя к переменной $x$, получаем $3^x ∈ [{1}/{3}; 9], x ∈ [-1; 2]$.
Задача 5
Решите неравенство ${45⋅ 2^x-90+45⋅ 2^{-x}} / {2^x+2+2^{-x}}-{21⋅ 2^x+21} / {2^x+1}⩽{2^{x+3}-8} / {2^x+1}$.
Решение
${45(2^x+2^{-x}-2)} / {2^x+2^{-x}+2}-{21(2^x+1)} / {2^x+1}⩽ {2^3(2^x-1)} / {2^x+1}$
Выполним преобразования, обозначим $2^x=t$, $t>0$
Тогда неравенство примет вид: ${45(t+{1} / {t}-2)} / {t+{1} / {t}+2}-{21(t+1)} / {t+1}⩽ {8(t-1)} / {t+1}$, ${45⋅ (t-1)^2} / {(t+1)^2}-21⩽ {8(t-1)} / {t+1}$, ${45(t-1)^2} / {(t+1)^2}-{8(t-1)} / {t+1}-21⩽0$, ${45(t-1)^2-8(t^2-1)-21(t+1)^2} / {(t+1)^2}⩽ 0$; $(t+1)^2>0$
Cледовательно, $45(t-1)^2-8(t^2-1)-21(t+1)^2⩽ 0$, $45t^2-90t+45-8t^2+8-21t^2-42t-21⩽ 0$, $16t^2-132t+32⩽ 0$, $16t^2-132t+32=0$, $4t^2-33t+8=0$, $D=33^2-32⋅ 4=961=31^2$. $t_{1, 2}={33±31} / {8}$, $t_1=8$; $t_2={2} / {8}={1} / {4}$
Решением неравенства $4t^2-33t+8⩽ 0$ будет $t∈ [{1} / {4};8]$, то есть, переходя к переменной $x$, получаем $2^x∈ [{1} / {4};8]$, $x∈ [-2;3]$.
Задача 6
Решите неравенство ${3log_{9}x+1}/{2log_{9}x+3}≤3-log_{9}x$.
Решение
Преобразуем исходное неравенство: ${(3log_9x +1)- (3-log_9x)(2log_9x + 3)}/{2log_9x +3} ≤ 0$.
Обозначим $log_9x = t$.
Тогда неравенство примет вид: ${3t + 1- (3-t)(2t+3)}/{2t+3} ≤ 0$.
${2t^2 − 8}/{2t +3} ≤ 0, {(t − 2)(t + 2)}/{t +{3}/{2}} ≤ 0.$
Последнее неравенство решим методом интервалов.
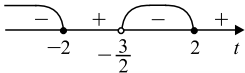
$(t − 2)(t + 2) = 0, t = -2; t = 2.$
$t +{3}/{2} ≠ 0, t ≠-{3}/{2}.$
Получим $t ∈ (−∞; -2] ∪ (-{3}/{2}; 2].$
Вернёмся к исходной переменной.
$[table{{tablelog_9x >-{3}/{2}; log_9x ≤2;}; log_9x ≤-2;$ $[table{{tablex >(9^{{3}/{2}})^{-1}; < x ≤ 81;}; < x ≤ 9^{-2};$
$[table{{tablex >(27)^{-1}; < x ≤ 81;}; < x ≤ {1}/{81};$ $[table{{tablex > {1}/{27}; < x ≤ 81;}; < x ≤ {1}/{81};$ $x ∈ (0; {1}/{81}] ∪ ({1}/{27}; 81].$
Задача 7
Решите неравенство ${11log_{4}x-28}/{2log_{4}x-1}≥4-3log_{4}x$.
Решение
Преобразуем исходное неравенство: ${11log_4x − 28 + (3log_4x − 4)(2log_4x − 1)}/{2log_4x − 1} ≥ 0$.
Обозначим $log_4x = t$.
Тогда неравенство примет вид: ${11t − 28 + 6t^2 − 11t + 4}/{2t − 1} ≥ 0$.
${6t^2 − 24}/{2t − 1} ≥ 0, {(t − 2)(t + 2)}/{t −{1}/{2}} ≥ 0.$
Последнее неравенство решим методом интервалов.
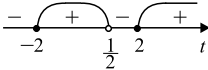
$(t − 2)(t + 2) = 0, t = 2; t = −2.$
$t −{1}/{2} ≠ 0, t ≠{1}/{2}.$
Получим $t ∈ [−2; {1}/{2}) ∪ [2; +∞).$
Вернёмся к исходной переменной.
$[table{{tablelog_4x ≥-2; log_4x <{1}/{2};}; log_4x ≥2;$ $[table{{tablex ≥{1}/{16}; < x < 4^{{1}/{2}};}; x ≥16;$
$[table{{tablex ≥{1}/{16}; < x < 2;}; x ≥16;$ $x ∈ [{1}/{16}; 2) ∪ [16; +∞).$
Задача 8
Решите неравенство ${1}/{log_{x}0.5}+6≥16log_{4x}2$.
Решение
ОДЗ уравнения ${tablex > 0; x≠1; x≠{1}/{4};$.
Т.к. ${1}/{log_x0.5}=-{1}/{log_x2}=-log_2x$, а $log_{4x}2 = {1}/{{log_{2} x} + 2}$, то неравенство примет вид $-log_{2}x + 6 ≥ {16}/{{log_{2}x} + 2}$. Пусть $log_2x = t$, тогда ${16}/{t +2}+t-6 ≤ 0, {(t − 2)^2}/{t + 2} ≤ 0, t = 2$ или $t < −2$.
$log_2x = 2$, откуда $x = 4$ или $log_2x < −2$, откуда $x < {1}/{4}$. Учитывая ОДЗ, получим $0 < x < {1}/{4}, x = 4$.
Задача 9
Решите неравенство $log_3(x — 1) ≤ 4 — 9 log_{9(x-1)}3$.
Решение
ОДЗ уравнения ${tablex-1 > 0; 9(x-1)≠1;$ то есть $x > 1, x ≠{10}/{9}$.
Используя формулу $log_ab ={log_cb}/{log_ca}$, получаем $log_{9(x−1)}3 = {1}/{log_3(x − 1) + 2}$.
Неравенство примет вид $log_3(x − 1) ≤ 4 − {9}/{log_3(x − 1) + 2}$. Пусть $log_3(x − 1) = t$, тогда $t − 4 + {9}/{t + 2} ≤ 0, {(t − 1)^2}/{t + 2} ≤ 0, t = 1$ или $t < −2$.
$log_3(x − 1) = 1$, откуда $x − 1 = 3, x = 4$ или $log_3(x − 1) < −2$, откуда $x − 1 < {1}/{9}, x < {10}/{9}$. Учитывая ОДЗ, получим $1 < x < {10}/{9}, x = 4$.
Задача 10
Решите неравенство $2 log_{x}3 + 3log_{3x}3 ≤ 2$.
Решение
Заметим, что $x > 0, x ≠ {1}/{3}, x ≠ 1$.
Используя свойства логарифмов, преобразуем неравенство:
${2}/{log_{3}x} + {3}/{log_{3}3x} ≤ 2,$
${2}/{log_{3}x} + {3}/{log_{3}3 + log_{3}x} ≤ 2,$
${2}/{log_{3}x} + {3}/{1 + log_{3}x} ≤ 2$
Пусть $log_{3}x = t$, тогда получим неравенство, которое удобно решить методом интервалов:
${2}/{t} + {3}/{1 + t} ≤ 2$,
${2(1 + t) + 3t − 2t(1 + t)}/{t(1 + t)} ≤ 0$,
${2t^2 − 3t − 2}/{t(1 + t)} ≥ 0$,
${(2t + 1)(t − 2)}/{t(t + 1)} ≥ 0.$
Получим два простых неравенства и одно двойное, решим их, возвращаясь к переменной $x$:
$t < -1, −{1}/{2}≤t<0, t ≥ 2,$
$log_3x < -1, log_3 {1}/{√3} ≤ log_3x < log_{3}1, log_{3}x ≥ log_{3}9,$
$0 < x<{1}/{3}, {1}/{√3}≤ x <1, x≥9.$
Так как найденные значения переменной удовлетворяют ОДЗ, то решение неравенства — $(0; {1}/{3})∪[{1}/{√3};1) ∪ [9; +∞)$.
Задача 11
Решите неравенство $(x^2+2x-3)log_{2x-1}(4x^2-11x+7)≤0$.
Решение
$(x^2 + 2x − 3) log_{2x−1}(4x^2 − 11x + 7) ≤ 0$
ОДЗ: ${table2x − 1 > 0; 2x − 1 ≠ 1; 4x^2 − 11x + 7 > 0;$ ${tablex > {1}/{2}; x ≠ 1; [tablex < 1; x > {7}/{4};$ $x ∈({1}/{2}; 1)∪({7}/{4}; +∞)$
Применяя метод рационализации, получим, что на ОДЗ исходное неравенство равносильно неравенству:
$(x^2 + 2x − 3)(2x − 1 − 1)(4x^2 − 11x + 7 − 1) ≤ 0;$
$(x − 1)(x + 3)(2x − 2)(4x^2 − 11x + 6) ≤ 0;$
$(x − 1)^2(x + 3)(x − 2)(x − {3}/{4})≤ 0.$
Из рисунка следует, что ${3}/{4}≤ x < 1; {7}/{4} < x ≤ 2$.
Задача 12
Решите неравенство $6^x√{15-x^2-2x}≥36√{15-x^2-2x}$.
Решение
Будем использовать метод интервалов, предварительно найдя ОДЗ и нули левой части неравенства. Преобразуем неравенство.
$(6^x-36)√{15 — x^2 — 2x} ≥ 0$
Найдём ОДЗ неравенства:
$-x^2 — 2x + 15 ≥ 0; x^2 + 2x — 15 ≤ 0; (x — 3)(x + 5) ≤ 0; x ∈ [-5; 3].$
Выражение $√{15 — x^2 — 2x}$ неотрицательно при любом допустимом значении $x$, значит неравенство выполняется при $6^x ≥ 36, 6^x ≥ 6^2, x ≥ 2$, а также если $√{15 — x^2 — 2x}=0; x^2 + 2x — 15 = 0; x_1 = -5, x_2 = 3$.
Учтём ОДЗ и найдём знаки левой части неравенства.
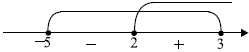
$x ∈ [2; 3] ∪$ {$-5$}.
Задача 13
Решите неравенство $log_{|x-2|}(4 + 7x — 2x^2)≥2$.
Решение
$log_{|x-2|}(4 + 7x−2x^2) ≥ 2$.
ОДЗ:
${table 4 + 7x−2x^2 > 0; x -2≠0; {|x -2|} ≠ 1;$
${table 2x^2 −7x−4 < 0; x≠2; x≠3; x≠1;$
${table (x + 0.5)(x−4) < 0; x≠2; x≠3; x≠1;$
$x ∈ (−0.5;1)∪(1;2)∪(2;3)∪(3;4)$.
$log_{|x-2|}(4 + 7x−2x^2) ≥ log_{|x-2|}(x -2)^2$.
$log_{|x-2|}(4 + 7x−2x^2)−log_{|x-2|}(x -2)^2 ≥ 0$.
На ОДЗ заменим полученное неравенство равносильными неравенствами, применив дважды метод рационализации:
1) знак $log_{a}f −log_{a}g$ совпадает со знаком $(a−1)(f −g)$.
2) знак $|f|−|g|$ совпадает со знаком $(f − g)(f + g)$.
Применяем 1: $(|x -2|−1)(4 + 7x−2x^2 −x^2 +4x−4) ≥ 0, (|x -2|−1)(−3x^2 + 11x) ≥ 0$.
Разделим обе части неравенства на $−3$.
$(|x -2|−1)(x^2 −{11x}/{3}) ≤ 0$.
Применяем 2: $(x -2−1)(x -2 + 1)x(x−{11}/{3}) ≤ 0, x(x — 3)(x -1)(x−{11}/{3}) ≤ 0$.
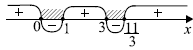
$0 ≤ x ≤ 1, 3 ≤ x ≤ {11}/{3}$.
Учитывая ОДЗ, получим:
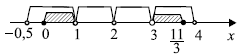
$0 ≤ x < 1; 3< x ≤ {11}/{3}$.
Задача 14
Решите неравенство $log_{|x+4|}(16 + 14x — 2x^2) ≥ 2$.
Решение
$log_{|x+4|}(16 + 14x−2x^2) ≥ 2$.
ОДЗ:
${table 16 + 14x−2x^2 > 0; x + 4≠0; {|x + 4|} ≠ 1;$
${table x^2 −7x−8 < 0; x≠−4; x≠−3; x≠−5;$
${table (x + 1)(x−8) < 0; x≠−4; x≠−3; x≠−5;$
$x ∈ (−1;8)$.
$log_{|x+4|}(16 + 14x−2x^2) ≥ log_{|x+4|}(x + 4)^2$.
$log_{|x+4|}(16 + 14x−2x^2)−log_{|x+4|}(x + 4)^2 ≥ 0$.
На ОДЗ заменим полученное неравенство равносильными неравенствами, применив дважды метод рационализации:
1) знак $log_{a}f −log_{a}g$ совпадает со знаком $(a−1)(f −g)$.
2) знак $|f|−|g|$ совпадает со знаком $(f − g)(f + g)$.
Согласно 1: $(|x + 4|−1)(16 + 14x−2x^2 −x^2 −8x−16) ≥ 0, (|x + 4|−1)(−3x^2 + 6x) ≥ 0$.
Разделим обе части неравенства на $−3$.
$(|x + 4|−1)(x^2 −2x) ≤ 0$.
Согласно 2: $(x + 4−1)(x + 4 + 1)x(x−2) ≤ 0, x(x + 3)(x + 5)(x−2) ≤ 0$.
$−5 ≤ x ≤ −3, 0 ≤ x ≤ 2$.
Учитывая ОДЗ, получим:
$0 ≤ x ≤ 2$.
Задача 15
Решите неравенство ${35·3^x}/{4+10·3^x-6·3^{2x}}≥{3^x+2}/{3^{x+1}+1}-{3^{x+1}-1}/{3^x-2}$.
Решение
С помощью замены $3^x = t$, где $t > 0$ приведём неравенство к виду
${35t}/{4 + 10t — 6t^2} ≥ {t + 2}/{3t + 1}- {3t — 1}/{t — 2}$.
$-6t^2 + 10t + 4 = -2(3t^2 — 5t — 2) = -2(t — 2)(3t + 1)$.
${35t}/{-2(t — 2)(3t + 1)} ≥ {(t + 2)(t — 2) — (3t — 1)(3t + 1)}/{(3t + 1)(t — 2)}$
${35t}/{-2(t — 2)(3t + 1)} ≥ {(t^2 — 4) — (9t^2 — 1)}/{(3t + 1)(t — 2)}$
${35t}/{-2(t — 2)(3t + 1)} ≥ {-8t^2 — 3}/{(3t + 1)(t — 2)};$
${35t}/{(t — 2)(3t + 1)} ≤ {16t^2 + 6}/{(3t + 1)(t — 2)};$
${16t^2 — 35t + 6}/{(3t + 1)(t — 2)}≥ 0;$
${16(t — 2)(t — {3}/{16})}/{(3t + 1)(t — 2)}≥ 0;$
${(t — {3}/{16})}/{(3t + 1)} ≥ 0, t ≠ 2.$
$t < -{1}/{3}$ или ${3}/{16} ≤ t < 2, t > 2$. С учётом условия $t > 0, {3}/{16} ≤ t < 2, t > 2$. Возвращаясь к переменной $x$, получим, что ${3}/{16} ≤ 3^x < 2$ или $3^x > 2$, откуда $log_3{3}/{16} ≤ x < log_{3}2$ или $x > log_{3}2$.
Задача 16
Решите неравенство ${4^{x}+27·2^{x}+18}/{2^{2x}+8·2^{x}+12}≥1+2^{x}-{2^{x}-3}/{2^{x}+6}$
Решение
${4^x + 27·2^x + 18}/{2^{2x} + 8·2^x + 12} ≥ 1 + 2^x — {2^x — 3}/{2^x + 6}$.
Обозначим $2^x = t, t > 0$. Неравенство примет вид:
${t^2 + 27t + 18}/{t^2 + 8t + 12} ≥ 1 + t — {t — 3}/{t + 6}$,
${t^2 + 8t + 12 + 19t + 6}/{t^2 + 8t + 12} ≥ 1 + t — {t — 3}/{t + 6}$,
$1 + {19t + 6}/{(t + 2)(t + 6)} ≥ 1 + t — {t — 3}/{t + 6}$,
${19t + 6}/{(t + 2)(t + 6)} — t + {t — 3}/{t + 6} ≥ 0$,
$-{t(t^2 + 7t — 6)}/{(t + 2)(t + 6)} ≥ 0$.
Полученное неравенство при условии $t > 0$ равносильно неравенству $t^2 + 7t — 6 ≤ 0$ (так как $t> 0, t + 2 > 0$ и $t + 6 > 0$),
$0 < t ≤ {√{73} — 7}/{2}$,
$0 < 2^x ≤ {√{73} — 7}/{2}$,
$x ≤ log_2 {√{73} — 7}/{2}$.
Задача 17
Решите неравенство ${3^{2x}+2·3^{x}+2}/{3^{2x}+2·3^{x}}≤4+{1}/{3^x}-{3·3^{x}+1}/{3^{x}-1}$.
Решение
${3^{2x} + 2·3^x + 2}/{3^{2x} + 2·3^x} ≤ 4 + {1}/{3^x}-{3·3^x + 1}/{3^x — 1}$.
Обозначим $3^x = t, t > 0$. Неравенство примет вид:
${t^2 + 2t + 2}/{t^2 + 2t}≤4 + {1}/{t}-{3t + 1}/{t — 1}$,
$1 + {2}/{t(t + 2)} — 4 — {1}/{t} + {3t + 1}/{t — 1} ≤ 0$,
${3(t + 3)t}/{t(t — 1)(t + 2)} ≤ 0$. Воспользуемся условием $t > 0$.
Так как при этом $t + 3 > 0$ и $t + 2> 0$, то неравенство верно при $t — 1 < 0$, то есть $0 < t < 1$. Тогда $0 < 3^x < 1, x < 0$.
Задача 18
Решите неравенство $(3x — 7) log_{5x-11}(x^{2} — 8x + 17) ≥ 0$.
Решение
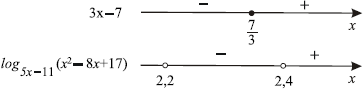
В правой части неравенства стоит $0$, в левой — произведение двух множителей. Определим знаки каждого из этих множителей.
При $x ={7}/{3}$ выражение $3x — 7 = 0$, при $x > {7}/{3}$ выражение $3x — 7 > 0$, а при $x < {7}/{3}$ выражение $3x — 7 < 0$.
Рассмотрим выражение $log_{5x-11}(x^2 — 8x + 17)$ и определим его знаки. Заметим, что $x^2 — 8x + 17 = (x — 4)^2 + 1 ≥ 1$ при любых значениях $x$. Значит, при $5x — 11 > 1$, то есть при $x > 2.4$, выражение $log_{5x-11}(x^2 — 8x + 17) > 0$; при $0 < 5x — 11 < 1$, то есть при $2.2 < x < 2.4, log_{5x-11}(x^2 — 8x + 17) < 0$ и не определено при $x ≤ 2.2$ и $x = 2.4$.
Удобно знаки сомножителей отметить на двух параллельных прямых.
Таким образом, решение исходного неравенства: ${11}/{5} < x ≤{7}/{3}; x > 2.4$.
Задача 19
Решите неравенство $(7x — 10) log_{4x-3}(x^{2} — 4x + 9) ≥ 0$.
Решение
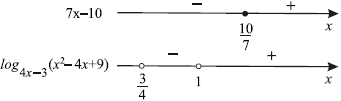
В правой части неравенства стоит $0$, в левой — произведение двух множителей. Определим знаки каждого из этих множителей.
При $x ={10}/{7}$ выражение $7x-10 = 0$, при $x > {10}/{7}$ выражение $7x-10 > 0$, а при $x < {10}/{7}$ выражение $7x — 10 < 0$.
Рассмотрим выражение $log_{4x-3}(x^2 — 4x + 9)$. Заметим, что $x^2 — 4x + 9 = (x — 2)^2 + 5 ≥ 5$ при любых значениях $x$. Значит, при $4x — 3 > 1$, то есть при $x > 1$, выражение $log_{4x-3}(x^2 — 4x + 9) >0$, при $0 < 4x — 3 < 1$, то есть при ${3}/{4} < x < 1, log_{4x-3}(x^2 — 4x + 9) < 0$ и не определено при $x ≤{3}/{4}$ и $x = 1$.
Удобно знаки сомножителей отметить на двух параллельных прямых.
Таким образом, решение исходного неравенства: ${3}/{4} < x < 1; x ≥ {10}/{7}$.
В задании №15 требуется решить один из видов неравенств:
- Рациональное неравенство
- Показательное неравенство
- Логарифмическое неравенство, возможно с переменным основанием
- Неравенство с радикалом
- Смешанное неравенство, которое может содержать несколько видов одновременно
Получить за решение этого задания можно 2 первичных балла. Потерять 1 балл можно при вычислительной ошибке, при условии что имеется верная последовательность всех шагов решения.
Метод интервалов
- Решить уравнение f(x) = 0. Так мы найдем нули функции, от которых зависит знак неравенства. Удобно отдельно находить нули числителя и нули знаменателя.
- Отметить все полученные корни (нули) на координатной прямой. Получим несколько интервалов.
- Выяснить знак (плюс или минус) функции f(x) на самом правом интервале. Для этого достаточно подставить в f(x) очень большое число, например, 1 000 000.
- Отметить знаки на остальных интервалах. Для этого достаточно запомнить, что при переходе через каждый корень знак меняется. НО есть одно исключение:
При переходе через нуль мы можем поменять знак на противоположный, если степень выражения, дающего этот нуль, нечетная, и не можем поменять знак, если степень четная.
Пример 1
При переходе через нуль мы можем поменять знак на противоположный, если степень выражения, дающего этот нуль, нечетная, и не можем поменять знак, если степень четная.
Пример 2
В случае с нестрогими неравенствами( ≤ , ≥) необходимо включить в интервалы точки, которые являются решением уравнения f(x) = 0;
Пример 3
Знак правого промежутка был «+». Единственный нуль четной степени x = 10, поэтому в этом нуле знак не меняем. В остальных нулях чередуем знак.
Пример неравенства №15
Еще больше крутых лайфхаков, разборов, ловушек ЕГЭ и теории в нашей группе вконтакте и инсте преподавателей @turboegemath и @turbomath