Задание 3. Стереометрия. ЕГЭ 2024 по математике профильного уровня
Средний процент выполнения: 95%
Ответом к заданию 3 по математике (профильной) может быть целое число или конечная десятичная дробь.
Задачи для практики
Задача 1
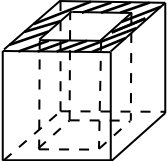
Из единичного куба вырезана правильная четырёхугольная призма со стороной основания $0{,}7$ и боковым ребром $1$. Найдите площадь поверхности получившейся фигуры (cм. рис.).
Решение
Поверхность оставшейся части куба состоит из боковой поверхности куба, площадь которой равна 4·1·1=4, боковой поверхности призмы, площадь которой равна 4·0,7·1=2.8, и двух равных фигур (см. заштрихованную фигуру на рисунке), площадь каждой из которых равна 1·1 — 0,7·0,7 = 0.51. Таким образом, площадь поверхности оставшейся части куба равна 4 + 2.8 + 2 · 0.51 = 7.82.
Задача 2
Если каждое ребро куба увеличить на $1$ (см. рис.), то площадь его поверхности увеличится на $42$. Найдите ребро куба.
Решение
Пусть ребро куба равно $x$. Площадь поверхности куба равна $6x^2$. Если ребро куба увеличить на $1$, то оно станет равным $(x + 1)$, а площадь поверхности $6(x + 1)^2$. Так как площадь поверхности при этом увеличится на $42$, то $6(x + 1)^2 — 6x^2 = 42$, откуда $12x + 6 = 42, 12x = 36, x = 3$.
Задача 3
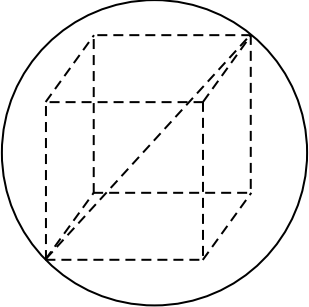
Куб вписан в шар радиуса $2√ 3$. Найдите объём куба.
Решение
Так как диагональ куба, вписанного в шар, равна диаметру шара, то $√3a = 2R$, где $a$ — ребро куба, $R = 2√3$ — радиус шара. Тогда $a√3 = 4√3, a = 4$. Объём куба равен $a^3 = 64$.
Задача 4
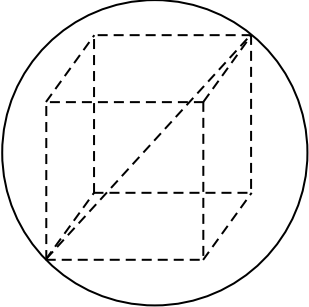
Куб вписан в шар радиуса $1{,}5√ 3$. Найдите объём куба.
Решение
Так как диагональ куба, вписанного в шар, равна диаметру шара, то $√3a = 2R$, где $a$ — ребро куба, $R = 1.5√3$ — радиус шара. Тогда $√3a = 3√3, a = 3$. Объём куба равен $a^3 = 27$.
Задача 5
Объём куба равен $64$ (см. рис.). Найдите площадь его поверхности.
Решение
Пусть ребро куба равно $x$. По условию объём куба равен $64$, тогда $x^3=64$, откуда $x=4$. Площадь грани куба равна $x^2=16$. Площадь поверхности куба равна $6x^2=6⋅16=96$.
Задача 6
Длина окружности основания цилиндра равна $6$. Площадь боковой поверхности равна $21$. Найдите высоту цилиндра.
Решение
Площадь боковой поверхности цилиндра вычисляется по формуле $S_{бок} = 2πRH$, где $R$ — радиус основания, $H$ — высота цилиндра. По условию $2πR = 6, S_{бок} = 21$, тогда $H = 21 : 6 = 3.5$.
Задача 7
В основании прямой призмы лежит ромб с диагоналями, равными $20$ и $48$ (см. рис.). Площадь её поверхности равна $1272$. Найдите боковое ребро этой призмы.
Решение
Так как диагонали ромба перпендикулярны и точкой пересечения делятся пополам, то сторону ромба найдём из прямоугольного треугольника $AOD$ по теореме Пифагора.
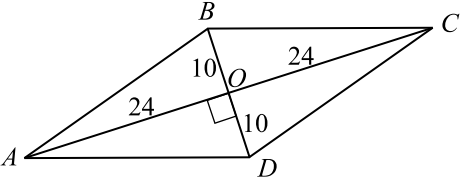
$AD = √{AO^2 + OD^2} = √{24^2 + 10^2} = 26$.
Площадь ромба $S_{осн} = {1}/{2}d_1 · d_2$, где $d_1$ и $d_2$ — диагонали ромба. $S_{осн} = {1}/{2} · 48 · 20 = 480$. Пусть боковое ребро призмы равно $x$. Площадь поверхности призмы равна $S = S_{бок} + 2S_{осн} = 1272$, откуда $S_{бок} = 1272 — 960 = 312$. Так как $S_{бок} = 4 · 26 · x$, то $104x = 312$, откуда $x = 3$.
Задача 8
В основании прямой призмы лежит ромб с диагоналями, равными $14$ и $48$ (см. рис.). Площадь её поверхности равна $1232$. Найдите боковое ребро этой призмы.
Решение
Так как диагонали ромба перпендикулярны и точкой пересечения делятся пополам, то сторону ромба найдём из прямоугольного треугольника $AOD$ по теореме Пифагора.
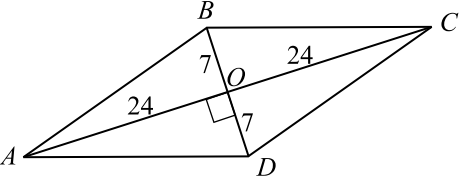
$AD = √{AO^2 + OD^2} = √{24^2 + 7^2} = 25$.
Площадь ромба $S_{осн} = {1}/{2}d_1 · d_2$, где $d_1$ и $d_2$ — диагонали ромба. $S_{осн} = {1}/{2} · 48 · 14 = 336$. Пусть боковое ребро призмы равно $x$. Площадь поверхности призмы равна $S = S_{бок} + 2S_{осн} = 1232$, откуда $S_{бок} = 1232 — 672 = 560$. Так как $S_{бок} = 4 · 25 · x$, то $100x = 560$, откуда $x = 5.6$.
Задача 9
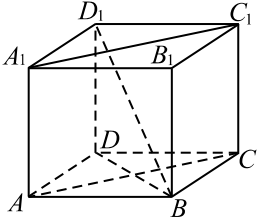
В правильной четырёхугольной призме $ABCDA_1B_1 C_1 D_1$ ребро $AA_1$ равно $24$, а диагональ $BD_1$ равна $26$ (см. рис.). Найдите площадь сечения призмы плоскостью, проходящей через точки $A$, $A_1$ и $C$.
Решение
Сечением призмы плоскостью, проходящей через точки $A, A_1$ и $C$, является прямоугольник $AA_1C_1C$, площадь которого равна $S = AA_1 · AC$. Выразим катет $BD$ из прямоугольного треугольника $BDD_1 : BD = √{BD_1^2 — DD_1^2} = √{26^2 — 24^2} = √{(26 — 24)(26 + 24)} = 10$. Так как $BD = AC$, то $S = 24 · 10 = 240$.
Задача 10
Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём цилиндра, если объём конуса равен $7$.
Решение
$V_{цилиндра}=S_{осн}⋅ H$, $V_{конуса}={1} / {3} S_{осн}⋅ H$. По условию конус
и цилиндр имеют общее основание и общую высоту, значит,
$V_{цилиндра}=3V_{конуса}=21$.
Задача 11
Найдите площадь поверхности правильной четырёхугольной пирамиды, стороны основания которой равны $24$ и высота равна $5$ (см. рис.).
Решение
Площадь $S$ поверхности правильной четырёхугольной пирамиды $SABCD$ равна сумме площади основания $S_{осн}$ и площади боковой поверхности $S_{бок}: S = S_{осн} + S_{бок} = AB^2 + 4S_{SBC}. SM$ — апофема.
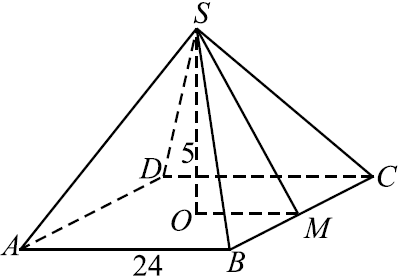
$S_{осн} = AB^2 = 576, SM$ найдём по теореме Пифагора как гипотенузу прямоугольного треугольника $SOM: SM = √{SO^2 + OM^2} = √{SO^2 + ({1}/{2}AB)^2} = √{5^2 + 12^2} = 13$.
$S_{бок} = 4S_{SBC} = 4·{1}/{2}·24·13 = 4·156=624. $
$S = 576 + 624 = 1200$.
Задача 12
Найдите площадь поверхности правильной четырёхугольной пирамиды, стороны основания которой равны $8$ и высота равна $3$ (см. рис.).
Решение
Площадь $S$ поверхности правильной четырёхугольной пирамиды $SABCD$ равна сумме площади основания $S_{осн}$ и площади боковой поверхности $S_{осн} + S_{бок} = AB^2 + 4S_{SBC}$
$SM$ — апофема.
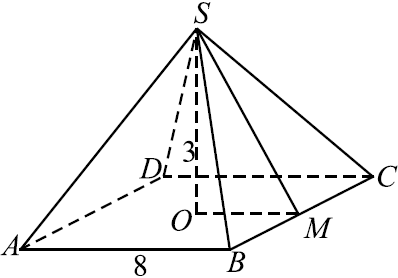
$S_{осн} = AB^2 = 64$
$SM$ найдём по теореме Пифагора как гипотенузу прямоугольного треугольника $SOM: SM = √{SO^2 + OM^2} = √{SO^2 + ({1}/{2}AB)^2} = √{3^2 + 4^2} = 5$.
$S_{бок} = 4S_{SBC} = 4·{1}/{2}·8·5 = 80$
$S_{осн} + S_{бок} = 64 + 80 = 144$
Задача 13
В правильной четырёхугольной пирамиде высота равна $3$, объём равен $32$ (cм. рис.). Найдите боковое ребро этой пирамиды.
Решение
Объём пирамиды вычисляется по формуле $V = {1}/{3}·S_{осн}·H$, где $H = 3$ — высота пирамиды. Площадь основания равна $S_{осн} = 3{V}/{H} = {3·32}/{3} = 32$, откуда длина стороны квадрата, лежащего в основании пирамиды, равна $√{32} = 4√2$. Диагональ квадрата $AC = 8$.
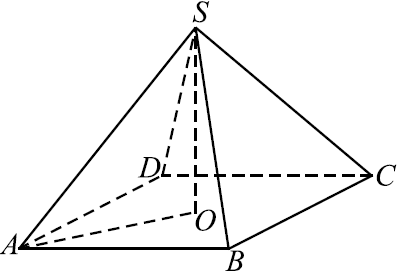
Боковое ребро $SA$ найдём как гипотенузу прямоугольного треугольника $AOS$, где $SO$ — высота пирамиды. $AS = √{SO^2 + OA^2} = √{SO^2 + ({1}/{2}AC)^2} = √{3^2 + 4^2} = 5$.
Задача 14
В правильной четырёхугольной пирамиде высота равна $9$, объём равен $864$ (cм. рис.). Найдите боковое ребро этой пирамиды.
Решение
Объём пирамиды вычисляется по формуле $V = {1}/{3}·S_{осн}·H$, где $H = 9$ — высота пирамиды. Площадь основания равна $S_{осн} = 3{V}/{H} = {3·864}/{9} = 288$, откуда длина стороны квадрата, лежащего в основании пирамиды, равна $√{288} = 12√2$. Диагональ квадрата $AC = 24$.
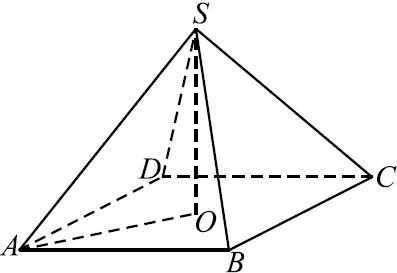
Боковое ребро $SA$ найдём как гипотенузу прямоугольного треугольника $AOS$, где $SO$ — высота пирамиды. $AS = √{SO^2 + OA^2} = √{SO^2 + ({1}/{2}AC)^2} = √{9^2 + 12^2} = 15$.
Задача 15
Площадь основания конуса равна $27$. Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки длиной $2$ и $4$, считая от вершины (см. рис.). Найдите площадь сечения конуса этой плоскостью.
Решение
Пусть $CA = R$ — радиус основания конуса, сечение конуса плоскостью, параллельной плоскости основания конуса — круг, радиус которого $OD = r$.
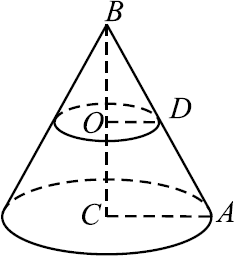
$OD ‖ AC$, следовательно, $△ABC ∼ △DBO$ по первому признаку подобия ($∠ACB = ∠DOB = 90°, ∠ABC$ — общий). По условию $BO = 2, OC = 4$, значит, $BC = 6$, откуда ${BO}/{BC} = {OD}/{AC} = {1}/{3}, {πr^2}/{πR^2} = {1}/{9}$. Значит, площадь сечения конуса плоскостью, параллельной плоскости основания конуса, в $9$ раз меньше плоскости основания конуса, то есть равна $27 : 9 = 3$.
Задача 16
Если каждое ребро куба увеличить на 3, то его площадь поверхности увеличится на 126. Найдите ребро куба.
Решение
$S_1=6а^2$
$ S_2=6(a+3)^2$
$ 6(a+3)^2-6а^2=126$
$ 6(а^2+6а+9)-6а^2=126$
$ 6а^2+36а+54-6а^2=126$
$ 36а=126-54$
$ 36а=72$
$ а=2$.