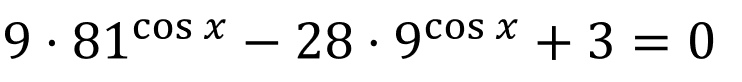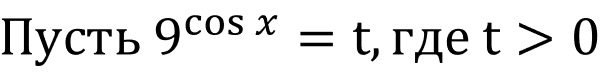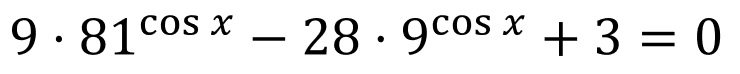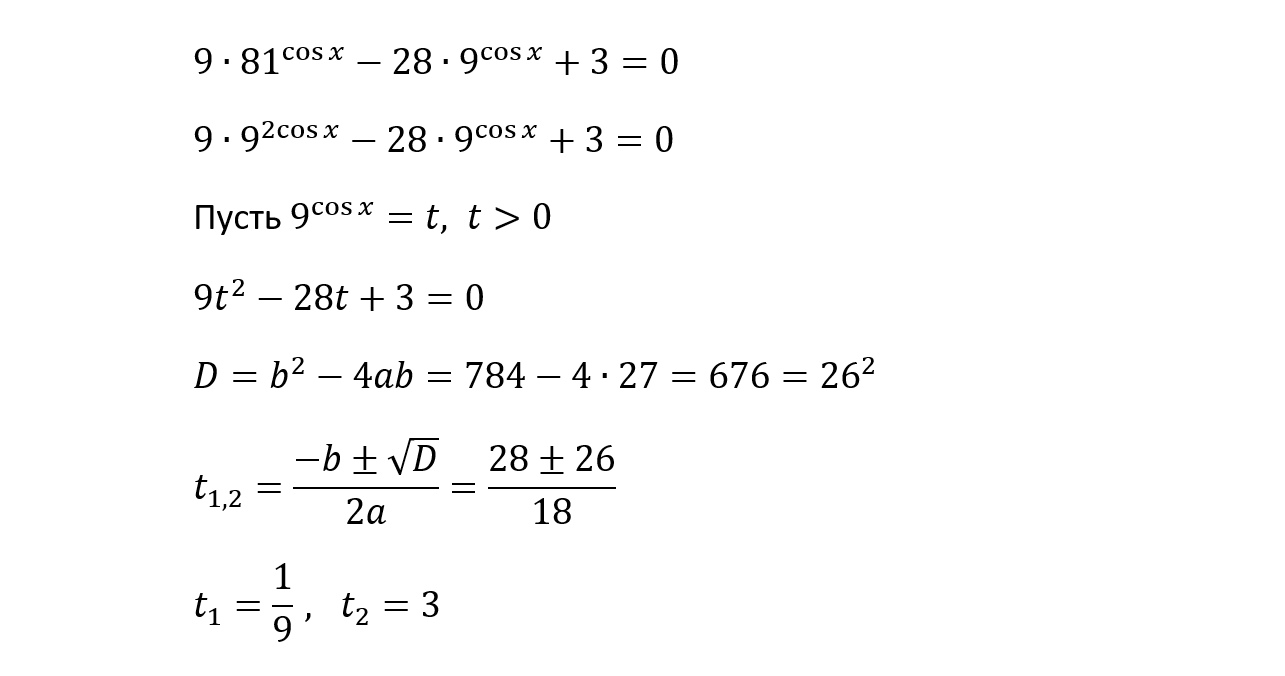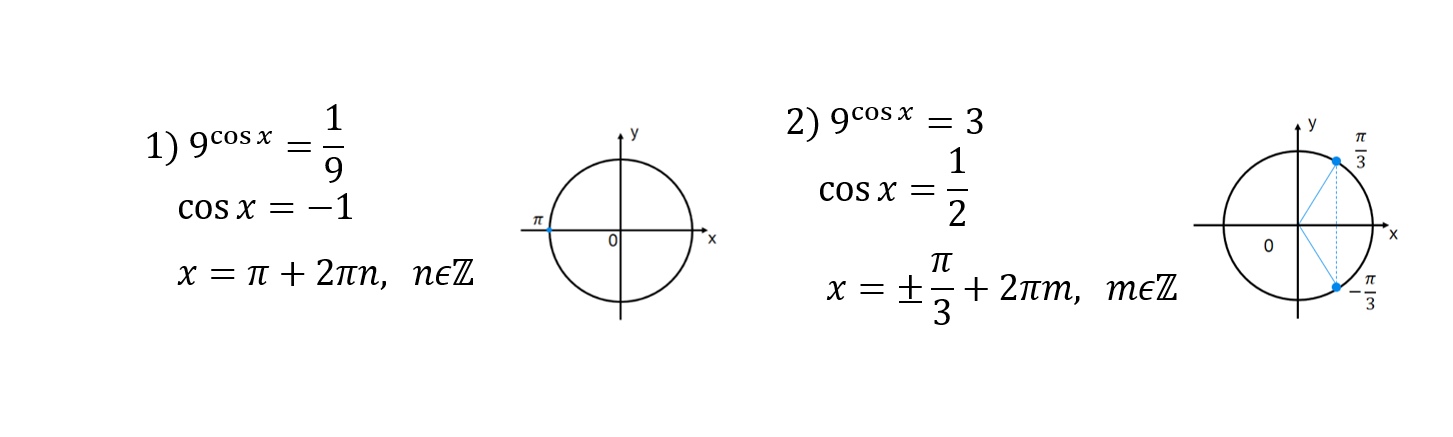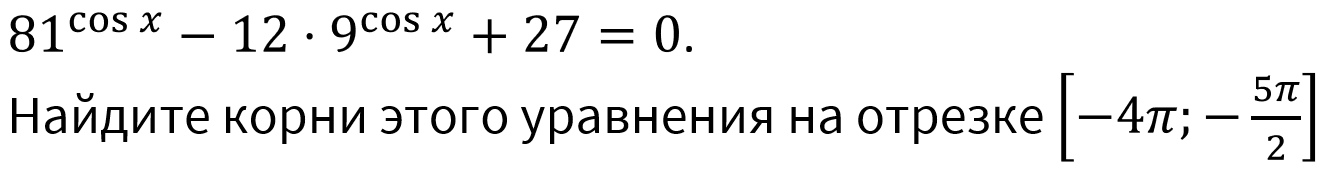- Задание 13. Уравнения. ЕГЭ 2024 по математике профильного уровня
- Что нужно знать, чтобы решить задание 13:
- Задачи для практики
- Задача 1
- Задача 2
- Задача 3
- Задача 4
- Задача 5
- Задача 6
- Задача 7
- Задача 8
- Задача 9
- Задача 10
- Задача 11
- Задача 12
- Задача 13
- Задача 14
- Задача 15
- Задача 16
- Задача 17
- Задача 18
- Задача 19
- Задача 20
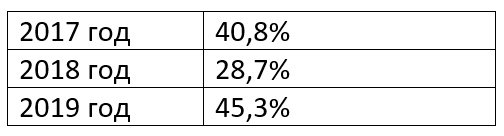
- Статистика
- Алгоритм решения задания №13
- Пример
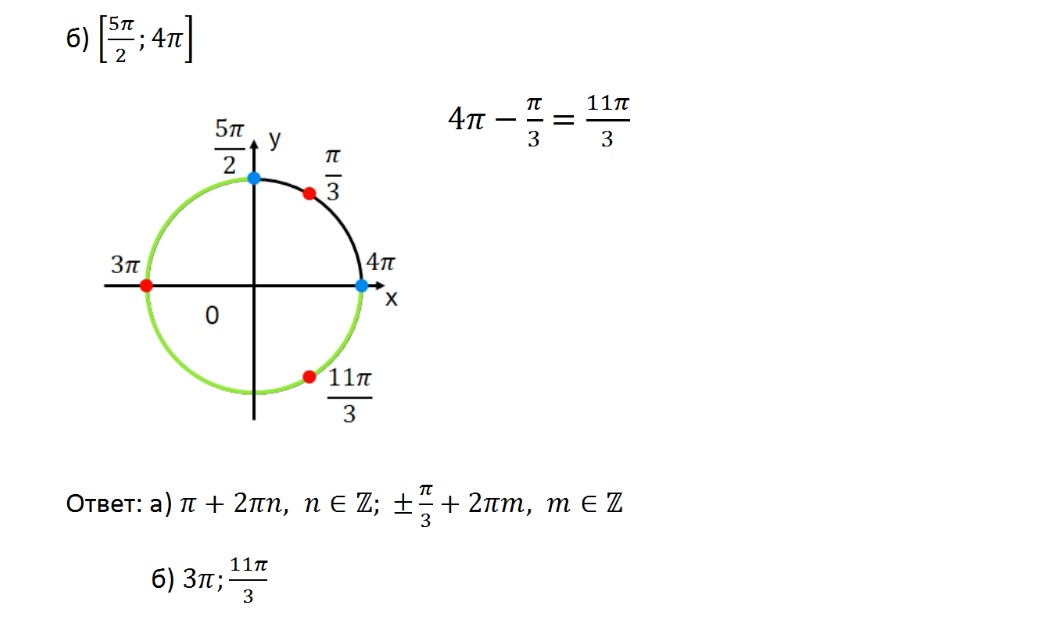
- Критерии отбора корней с помощью окружности
Задание 13. Уравнения. ЕГЭ 2024 по математике профильного уровня
Средний процент выполнения: 5.6%
Ответом к заданию 13 по математике (профильной) может быть развернутый ответ (полная запись решения с обоснованием выполненных действий).
Что нужно знать, чтобы решить задание 13:
В задании требуется решить уравнение одного из видов: тригонометрическое, рациональное, показательное, логарифмическое, уравнение с радикалом или смешанное уравнение, которое может содержать в себе несколько видов, например, логарифмы и тригонометрию. После решения уравнения, часто необходимо отобрать корни, которые принадлежат определенному промежутку.
Задачи для практики
Задача 1
а) Решите уравнение $11cos 2x=7sin (x-{π} / {2})-9$.
б) Укажите корни этого уравнения, принадлежащие отрезку $[-π;0]$.
Решение
а) $11cos 2x=7sin (x-{π} / {2})-9$,
$11(2cos^2 x-1)=-7cos x-9$,
$22cos^2 x -11+7cos x +9=0$,
$22cos^2 x+7cos x -2=0$.
Обозначим $cos x=t$, $|t|⩽1$.
Тогда уравнение примет вид: $22t^2+7t-2=0$.
Решим его. $22t^2+7t-2=0$,
$D=49+2⋅ 4⋅ 22=225$. $t_{1,2}={-7±15} / {44}$,
$t_1=-{1} / {2}$, $t_2={8} / {44}={2} / {11}$.
$1$. $cos x=-{1} / {2}$, $x=±(π-{π} / {3})+2π n$;
$x=± {2π} / {3}+2π n$, $n∈ Z$.
$2$. $cos x={2} / {11}$, $x=± arccos {2} / {11}+2π k$, $k∈ Z$.
б) Найдём корни этого уравнения, принадлежащие промежутку $[-π;0]$.
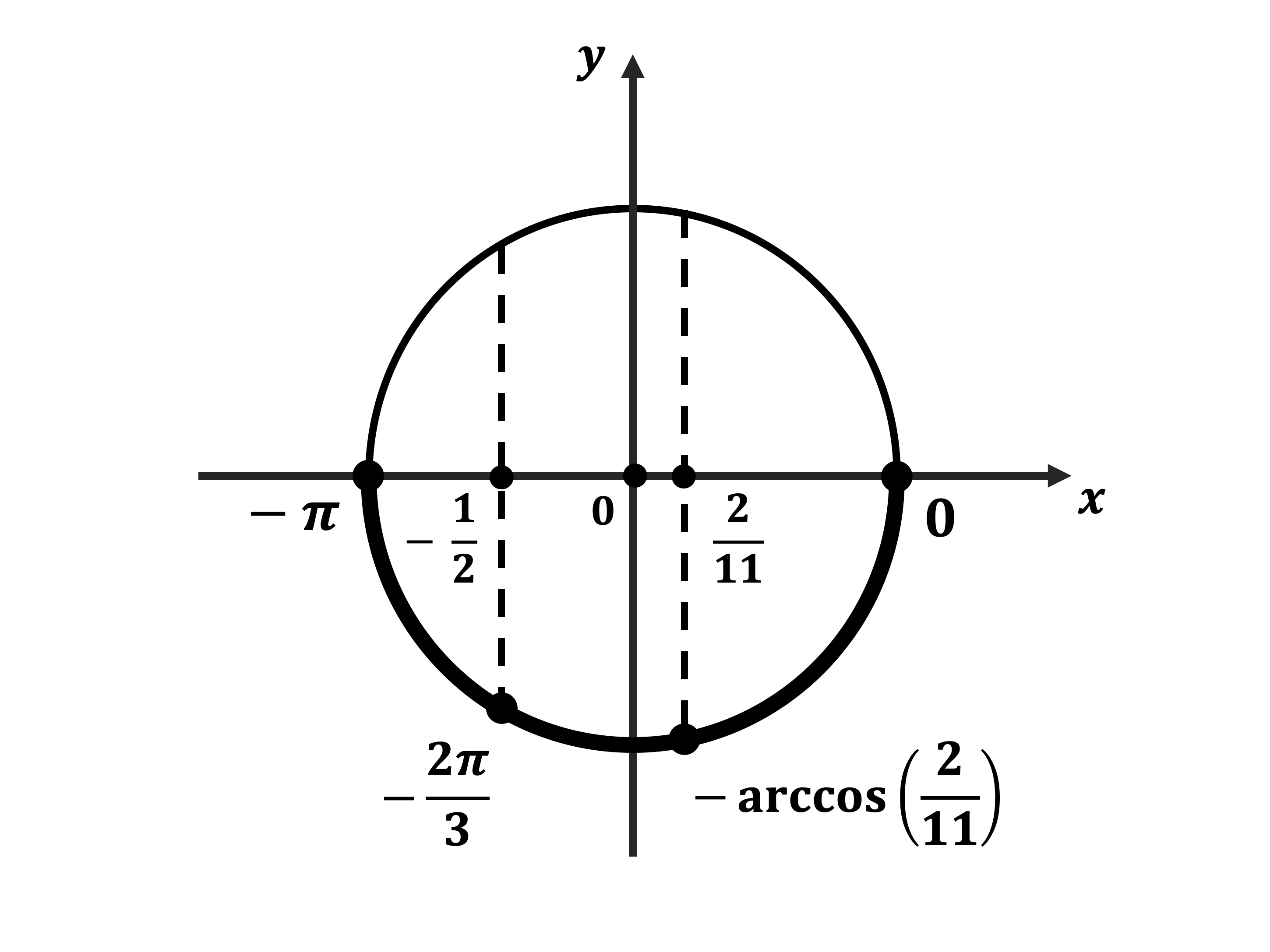
$x_1=-π+{π} / {3}=-{2π} / {3}$
$x_2=-arccos {2} / {11}$.
Задача 2
а) Решите уравнение $2 sin^2 x — 7 cos(x + {π}/{2})- 4 = 0$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $[-2π;-{π}/{2}]$.
Решение
а) Преобразуем уравнение, согласно формуле приведения:
$cos(x+{π}/{2})=-sinx,$
$2sin^2x + 7sinx -4 = 0$
Обозначим $sin x = t, −1 ≤ t ≤ 1$, получим
$2t^2 + 7t -4 = 0.$
$t_1 = {−7 − 9}/{2·2} = −4$ — не удовлетворяет условию $−1 ≤ t ≤ 1. $
$t_2 = {−7 + 9}/{2·2} = {1}/{2}$.
Вернёмся к исходной переменной:
$sinx ={1}/{2}$,
$x = {π}/{6} + 2πn, n ∈ Z$
$x = {5π}/{6} + 2πk, k ∈ Z$
б) Корни, принадлежащие отрезку $[-2π; -{π}/{2}]$, найдём с помощью единичной окружности. Получим: ${π}/{6}-2π=-{11π}/{6}; {5π}/{6}-2π=-{7π}/{6}$.
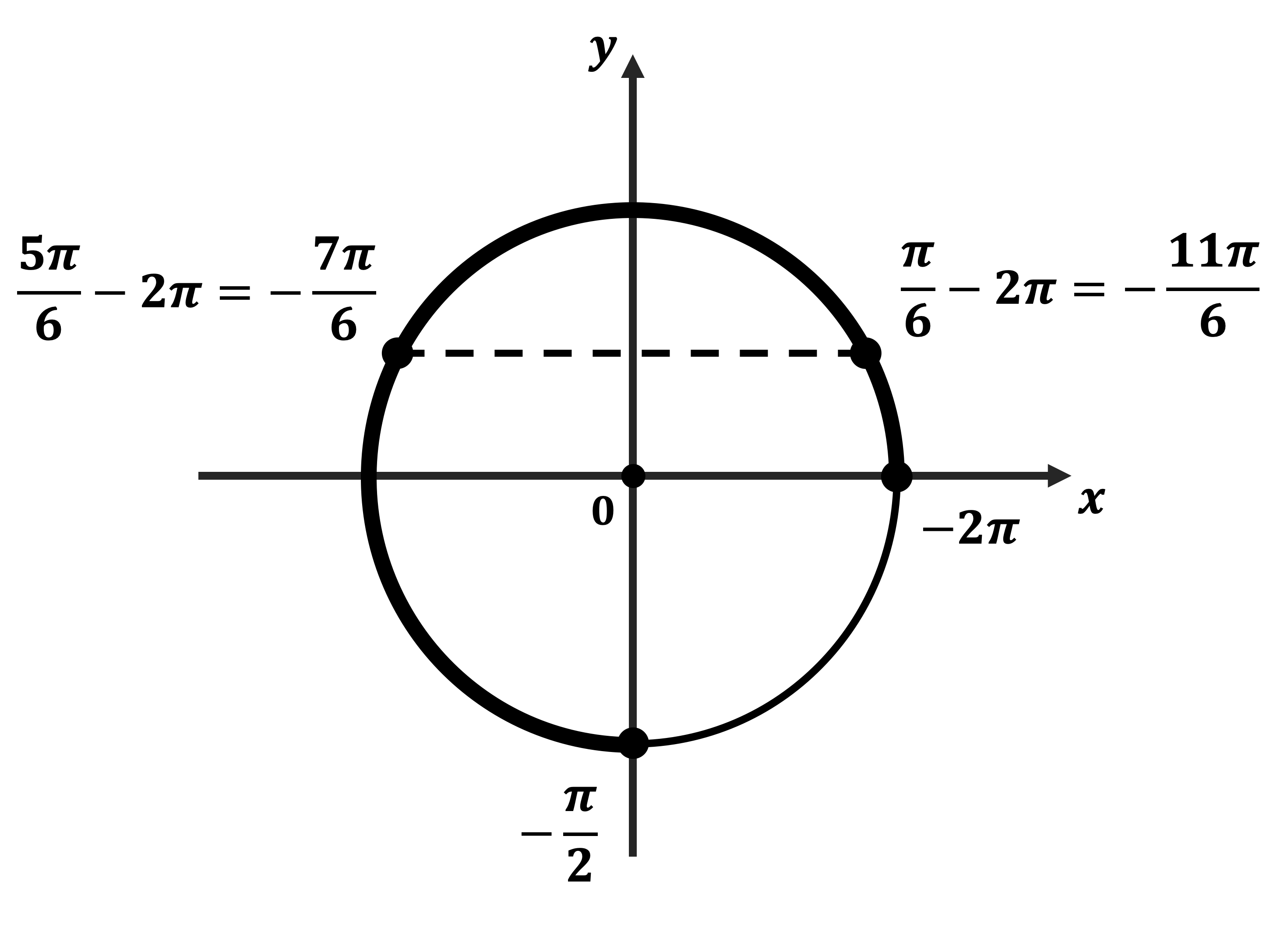
Задача 3
а) Решите уравнение $2 cos^2 x — 5 sin(x + {3π}/{2})+ 2 = 0$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $[{π}/{2};{3π}/{2}]$.
Решение
а) Преобразуем уравнение, согласно формуле приведения:
$sin(x+{3π}/{2})=-cosx,$
$2cos^2x + 5 cos x + 2 = 0$
Обозначим $cos x = t, −1 ≤ t ≤ 1$, получим $2t^2 + 5t + 2 = 0. t_1 = {−5 − 3}/{2·2} = −2$ — не удовлетворяет условию $−1 ≤ t ≤ 1. t_2 = {−5 + 3}/{2· 2} = −{1}/{2}$.
Вернёмся к исходной переменной: $cos x = − {1}/{2}$,
$x = ±(π − {π}/{3}) + 2πn, n ∈ Z , x = ±{2π}/{3} + 2πn, n ∈ Z.$
б) Корни, принадлежащие отрезку $[{π}/{2}; {3π}/{2}]$, найдём с помощью единичной окружности. Получим числа ${2π}/{3}; {4π}/{3}$.
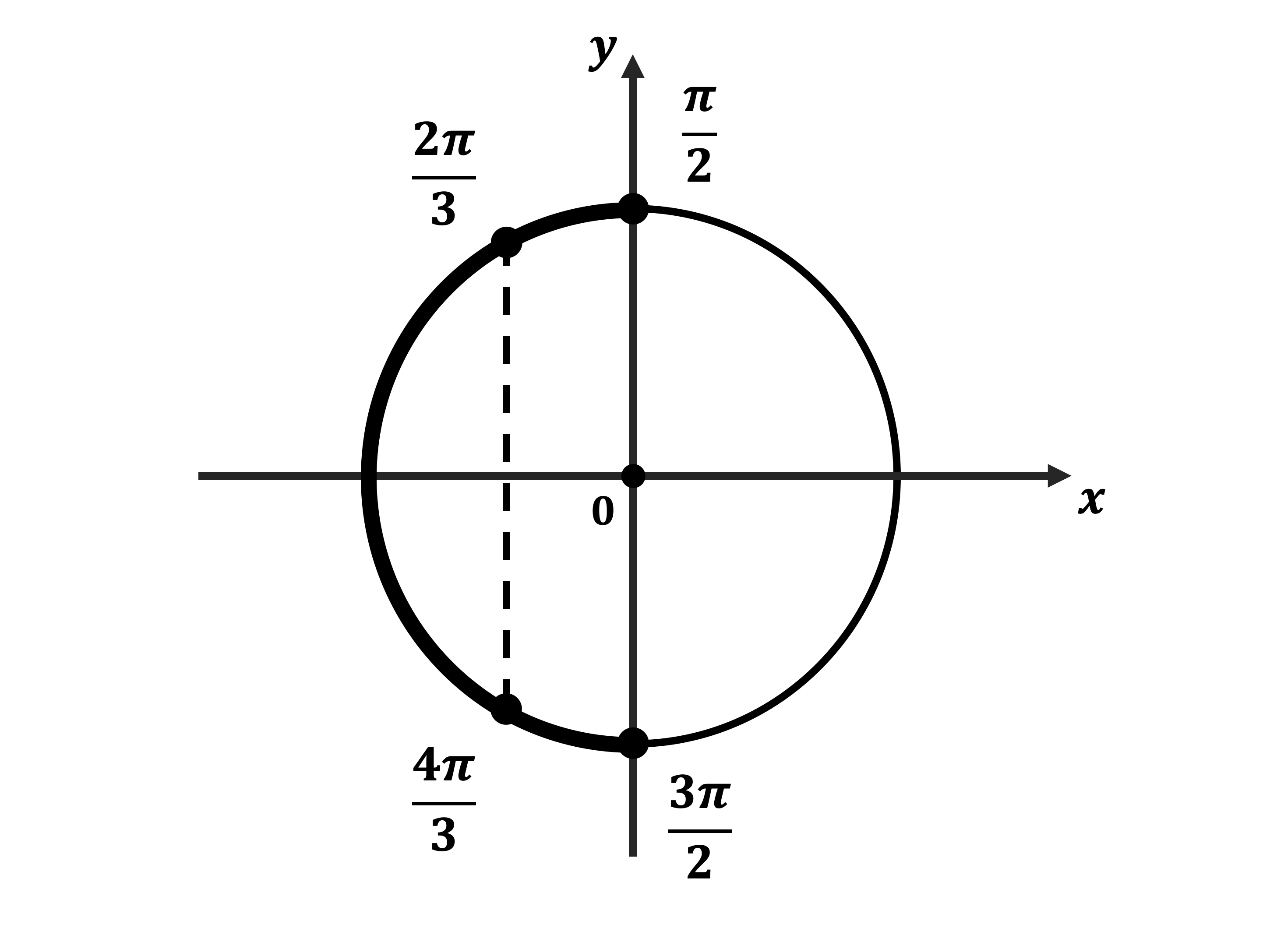
Задача 4
а) Решите уравнение $cos(x — {3π}/{2})= sin 2x$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $[-{3π}/{2};0]$.
Решение
а) Преобразуем уравнение:
$−sin x = sin 2x,$
$sinx + 2 sin x cos x = 0,$
$sinx(1 + 2 cos x) = 0,$
$sin x = 0;x = πn, n ∈ Z,$
$cosx = -{1}/{2}; x = ±{2π}/{3} + 2πk, k ∈ Z .,$
б) Корни, принадлежащие отрезку $[-{3π}/{2};0]$, найдём с помощью единичной окружности. Получим числа $−{4π}/{3}; −π; −{2π}/{3}; 0$.
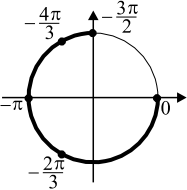
Задача 5
а) Решите уравнение $sin({π}/{2}+ x)= sin (-2x)$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $[0; π]$.
Решение
а) Преобразуем уравнение:
$cos x = − sin 2x,$
$cos x + 2 sin x cos x = 0,$
$cos x(1 + 2 sin x) = 0,$
$cos x = 0;$
$x = {π}/{2} + πn, n ∈ Z$
$sin x = −{1}/{2},$
$x = (−1)^{k+1}·{π}/{6} + πk, k ∈ Z$
б) Корни, принадлежащие отрезку $[0; π]$, найдём с помощью единичной окружности.
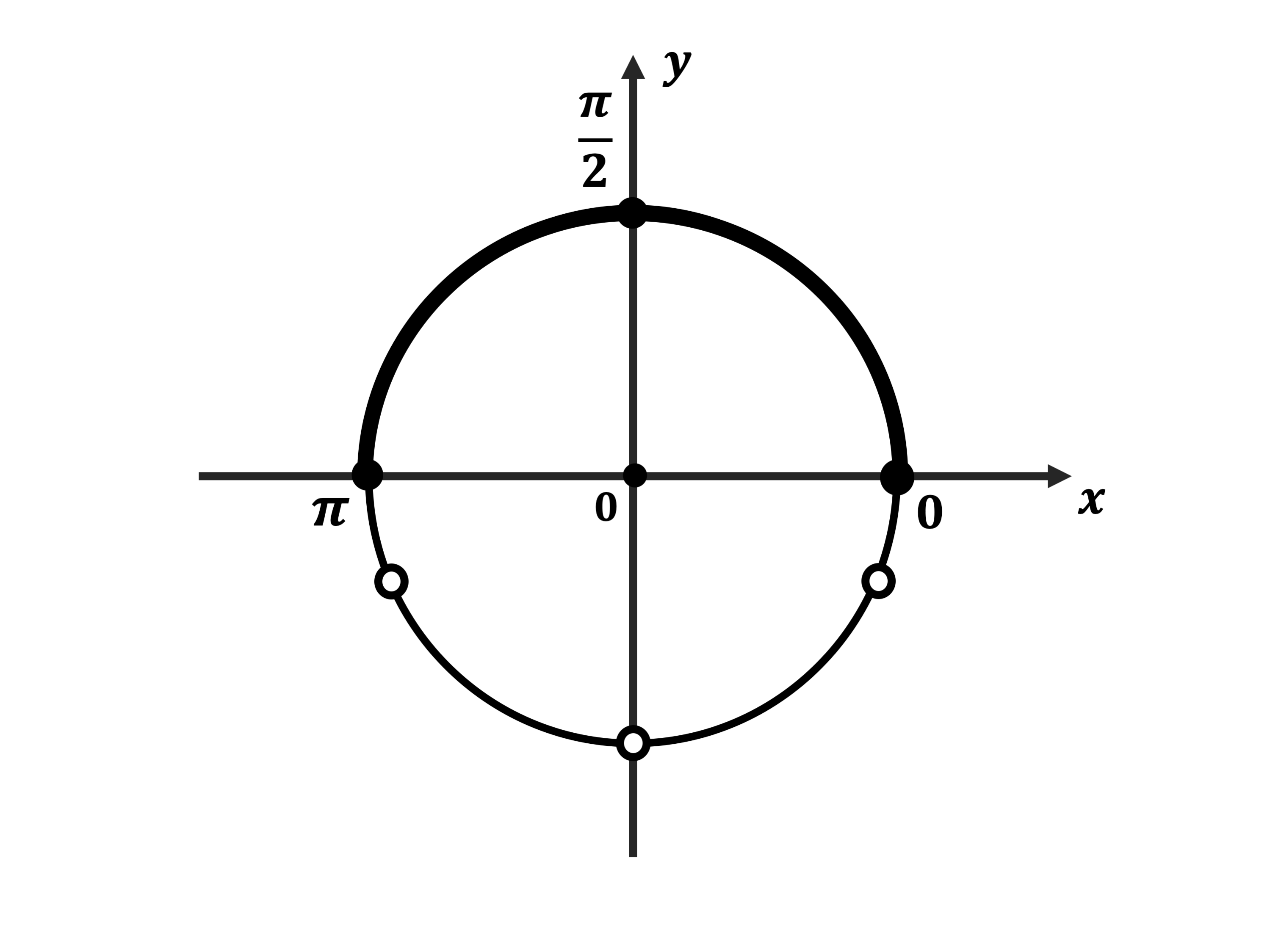
Указанному промежутку принадлежит единственное число ${π}/{2}$.
Задача 6
а) Решите уравнение $sin x(2 sin x — 1) + √3 sin x + sin {4π}/{3}= 0$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $[-{π}/{2};π]$.
Решение
а) Решим уравнение $sinx(2sinx-1) +√3sinx + sin{4π}/{3} = 0$.
Так как $sin{4π}/{3} = sin(π +{π}/{3}) = − sin{π}/{3} = −{√3}/{2}$, то уравнение примет вид $sin x(2 sin x-1) +√3 sin x-{√3}/{2} = 0$. Отсюда $2 sin x(sin x-{1}/{2})+ √3(sin x-{1}/{2}) = 0; (2sinx+√3)(sin x-{1}/{2}) = 0$.
Тогда $sin x = {1}/{2}; x = (−1)^n{π}/{6} + πn$ или $sin x = −{√3}/{2}; x = (−1)^{n+1}{π}/{3} + πn$, где $n ∈ Z.$
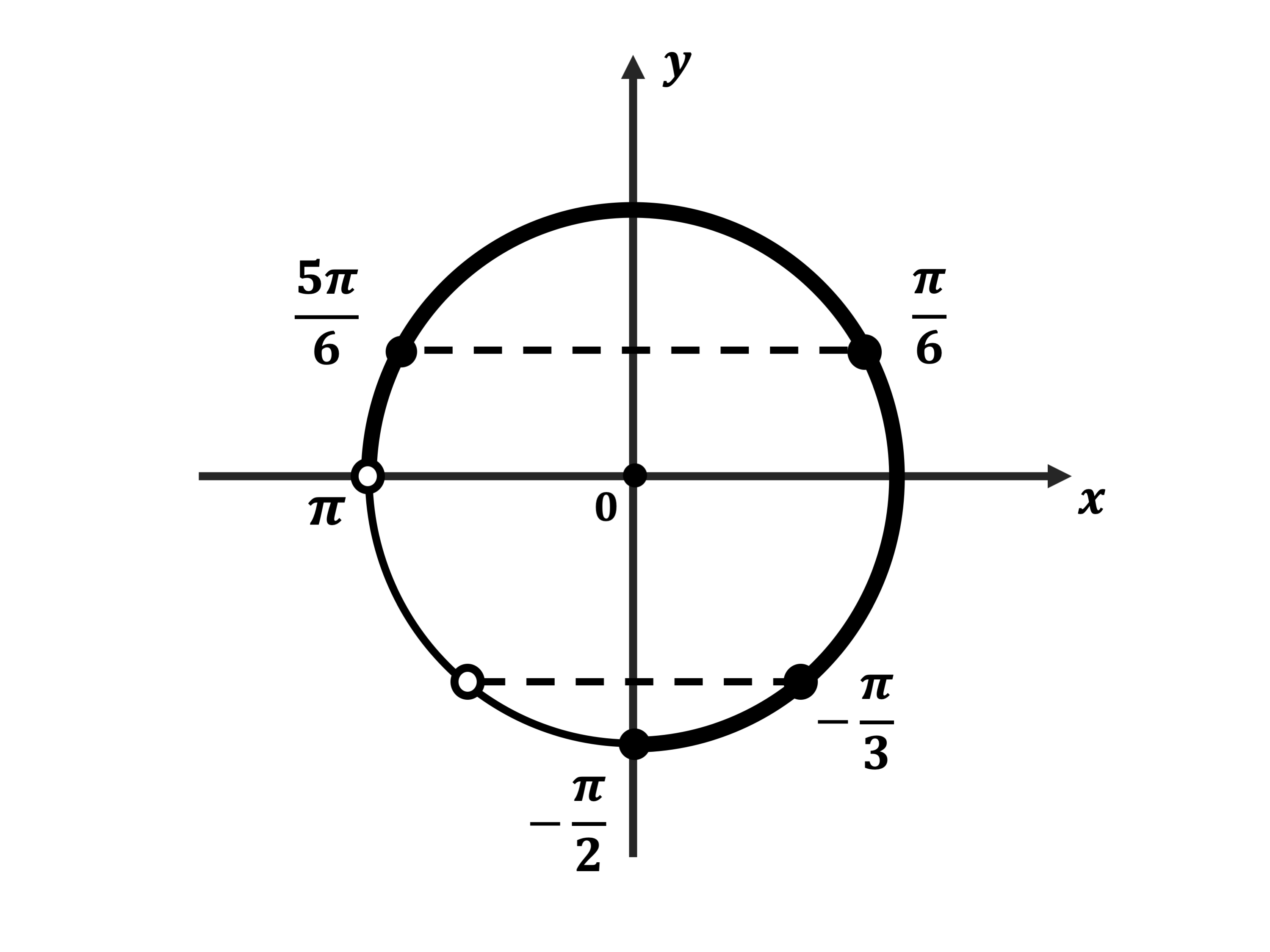
б) Корни, принадлежащие промежутку $[−{π}/{2}; π]$, найдём с помощью числовой окружности: $−{π}/{3}; {π}/{6}; {5π}/{6}$.
Задача 7
а) Решите уравнение $4cos^{2}x = 3cos2x + 1$.
б) Найдите корни уравнения, принадлежащие отрезку $[-4π;-{5π}/{4})$.
Решение
a) $4cos^{2}x = 3cos2x+1$,
$4cos^{2}x = 3(2cos^{2}x-1)+1$,
$4cos^{2}x=6cos^{2}x-3+1$,
$cos^{2}x=1, [tablecosx=1; cosx=-1;$ $[tablex=2πn, n ∈ Z; x=π+2πk, k ∈ Z;$ $x=πk, k ∈ Z$
б) Корни, принадлежащие промежутку $[-4π;-{5π}/{4})$, найдем из неравенства $-4π ≤ πk < -{5π}/{4}; k=-4, -3, -2$
$x_1=-4π, x_2=-3π, x_3=-2π$.
Задача 8
а) Решите уравнение $cos (2x) + 3 sin x — 2 = 0$.
б) Найдите корни уравнения, принадлежащие отрезку $[-3π;-π]$.
Решение
a) $cos(2x) + 3sinx-2=0$,
$1 — 2sin^{2}x + 3 sin x -2 = 0$,
$2 sin^{2}x — 3sin x +1 = 0$,
Пусть $sin x = y, |sinx| ≤ 1$, уравнение примет вид
$2y^2 — 3y + 1 = 0$,
$y_{1,2} = {3±√{9-8}}/{4} = {3±1}/{4};$
$ y_1=1, y_2={1}/{2}$.
$sin x = 1, x = {π}/{2}+2πn, n ∈ Z; sinx={1}/{2}, x=(-1)^{k}{π}/{6} + πk, k ∈ Z$.
б) Найдём корни уравнения на отрезке $[-3π;-π]$.
С помощью числовой окружности отберём корни уравнения, принадлежащие $[-3π;-π]$.
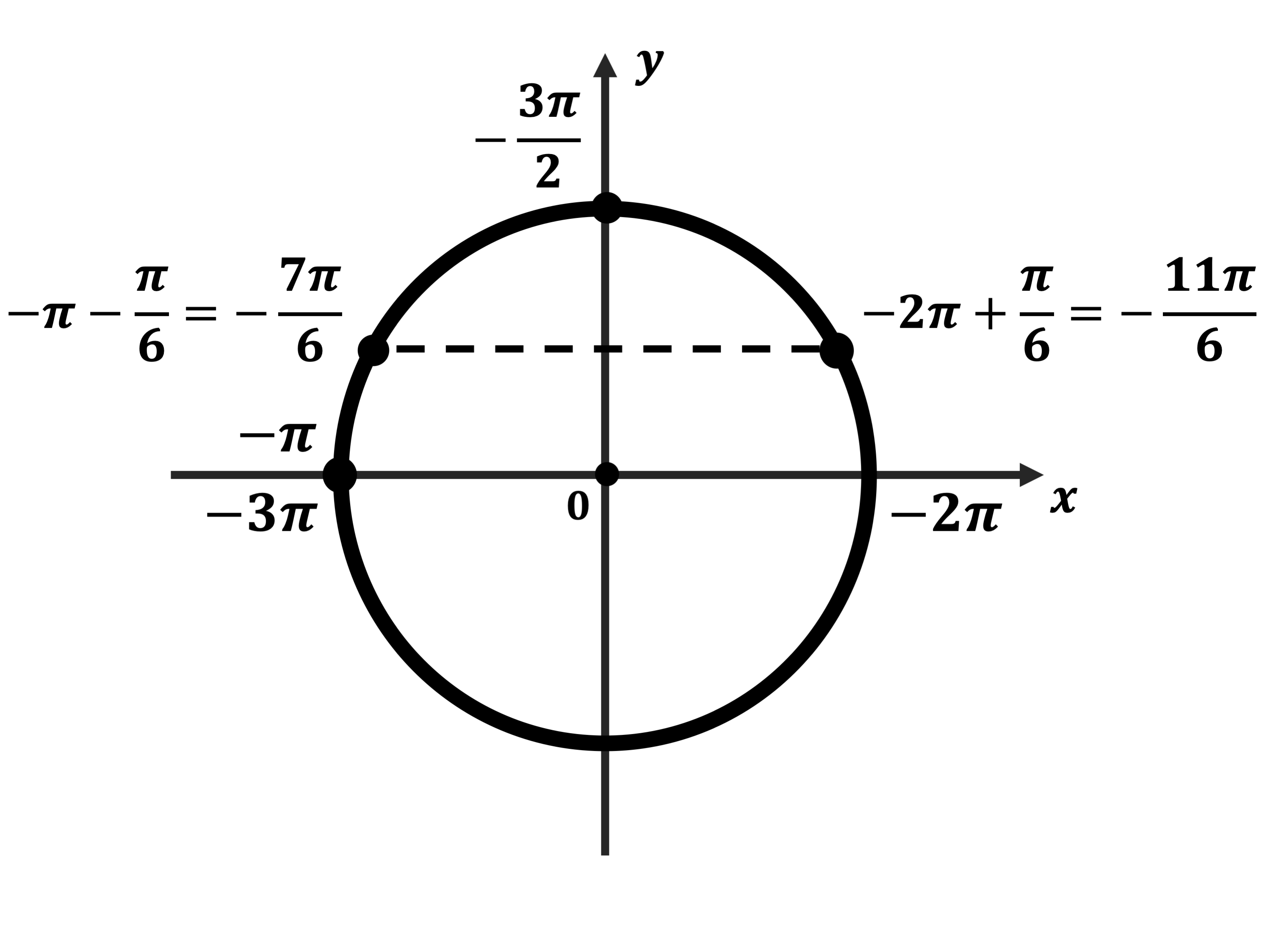
Это числа $-{11π}/{6}, -{3π}/{2}, -{7π}/{6}$.
Задача 9
а) Решите уравнение $2 cos^2 x + 19 sin x + 8 = 0$.
б) Найдите корни уравнения, принадлежащие отрезку $[-π;{π}/{2}]$.
Решение
a) $2 cos^{2}x + 19sinx+8=0$,
$2(1 — sin^{2}x) + 19 sin x +8 = 0$,
$-2 sin^{2}x + 19 sin x +10 = 0$,
$2 sin^{2}x — 19 sin x -10 = 0$.
Пусть $sin x = y, |y| ≤ 1$, уравнение примет вид $2y^2 — 19y -10 = 0$, решим его: $y_{1,2} = {19±√{361 + 80}}/{4} = {19±21}/{4}$.
$y_1 = 10$ или $y_2 = -{1}/{2}$. $y_1=10$ не удовлетворяет условию $|y| ≤ 1$. $sin x = -{1}/{2}, x = (-1)^{n+1}{π}/{6} + πn, n ∈ Z$.
б) Найдём корни уравнения на отрезке $[-π;{π}/{2}]$.
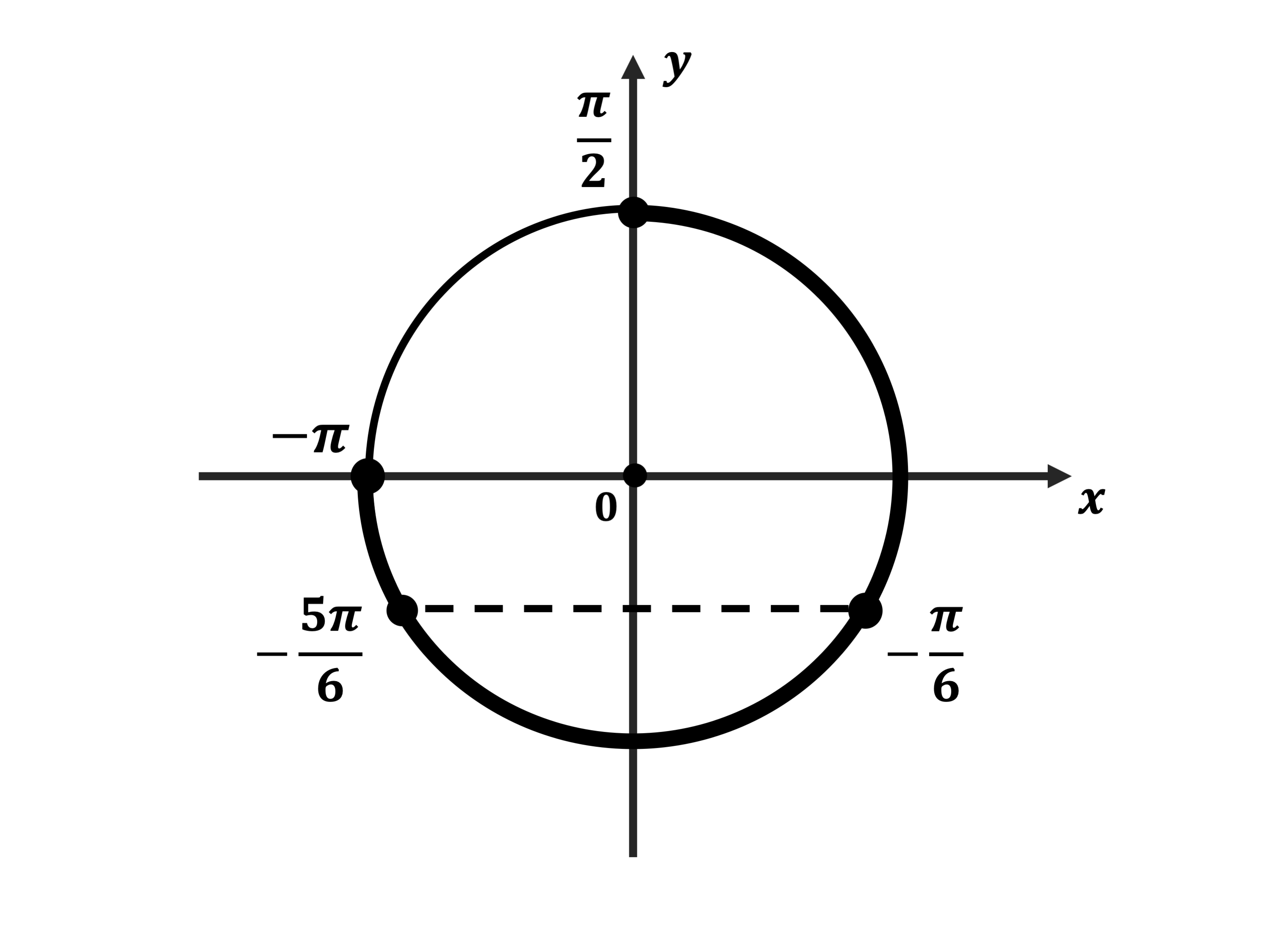
Это числа $-{5π}/{6}$ и $-{π}/{6}$.
Задача 10
а) Решите уравнение $8sin x + 4 cos^2 x = 7$.
б) Найдите корни уравнения, принадлежащие отрезку $[-{3π}/{2};-{π}/{2}]$.
Решение
a) $8 sin x + 4 cos^{2} x = 7$,
$4(1 — sin^{2}x) + 8 sin x — 7 = 0$,
$-4 sin^{2}x + 8 sin x — 3 = 0$,
$4 sin^{2}x — 8 sin x + 3 = 0$.
Пусть $sin x = t, |t| ≤ 1$, уравнение примет вид $4t^2 — 8t + 3 = 0$, решим его: $t_{1,2} = {8±√{64 — 48}}/{8} = {8±√{16}}/{8} = {8±4}/{8} = 1±{1}/{2}$.
$t_1 = {1}/{2}$ или $t_2 = {3}/{2}$. $t_2$ не удовлетворяет условию $|t| ≤ 1$. $sin x = {1}/{2}, x = (-1)^{n}{π}/{6} + πn, n ∈ Z$.
б) Найдём корни уравнения на отрезке $[-{3π}/{2};-{π}/{2}]$.
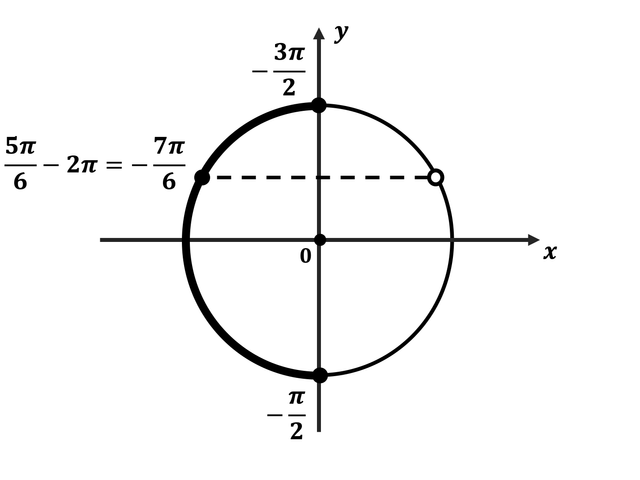
Это число ${5π}/{6} — 2π = -{7π}/{6}$.
Задача 11
а) Решите уравнение ${sin 2x}/{sin({3π}/{2}+ x)}= 1$.
б) Укажите корни этого уравнения, принадлежащие промежутку $(3π;{9π}/{2})$.
Решение
а) ${{sin2x}/{sin({3π}/{2} + x)} = 1$.
Зная, что $sin2x = 2sinxcosx$ и $sin({3π}/{2}+ x)= −cosx$, получим: ${2sinxcosx}/{−cosx}= 1$, где $cosx≠0, x≠{π}/{2}+ πm, m ∈ Z$.
$−2sinx = 1, sinx =−{1}/{2}$.
$x=−{π}/{6}+2πn, n ∈ Z;$
$x=-{5π}/{6}+ 2πk, k ∈ Z$.
б) Отберём корни уравнения, принадлежащие промежутку $(3π; {9π}/{2})$,с помощью числовой окружности.
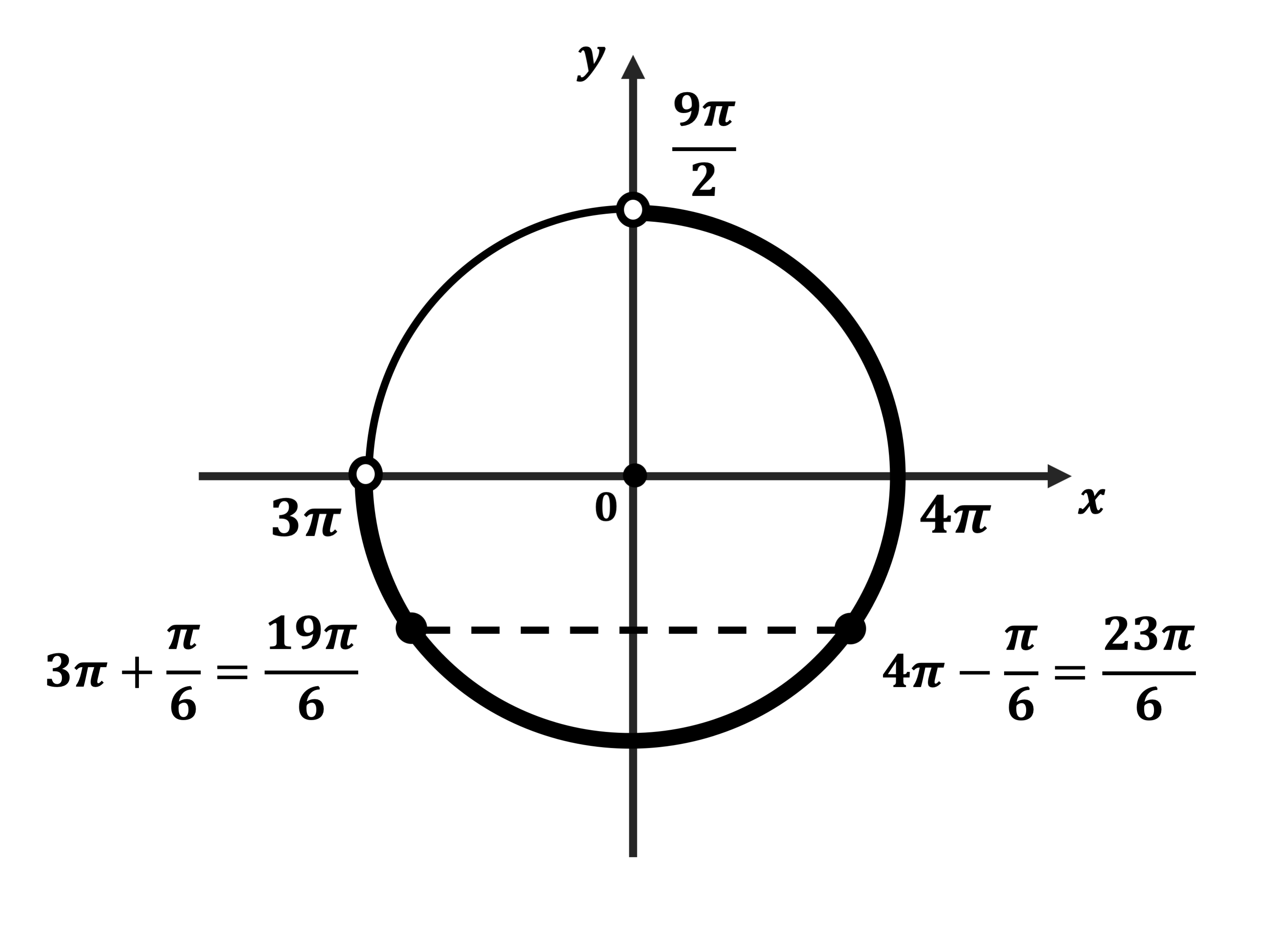
$x_1=3π+{π}/{6}={19π}/{6}$,
$x_2=4π−{π}/{6}={23π}/{6}$.
Задача 12
а) Решите уравнение ${sin 2x}/{sin(π — x)}= √2$.
б) Укажите корни этого уравнения, принадлежащие промежутку $[-{5π}/{2};-π)$.
Решение
а)${sin2x}/{sin(π — x)}=√2$.
а) Применим формулу синуса двойного аргумента $sin2x = 2sinxcosx$ и формулу приведения $sin(π — x) = sin x$.
Уравнение примет вид: ${2sinxcosx}/{sinx} = √2$.
Учитывая, что $sinx≠0, x≠πn, n∈Z$, получим:
$2cosx=√2$,
$cosx = {√2}/{2}$,
$x = ±{π}/{4} + 2πk, k∈Z$;
б) Отберём корни уравнения, принадлежащие промежутку $[-{5π}/{2};-π)$, с помощью окружности.
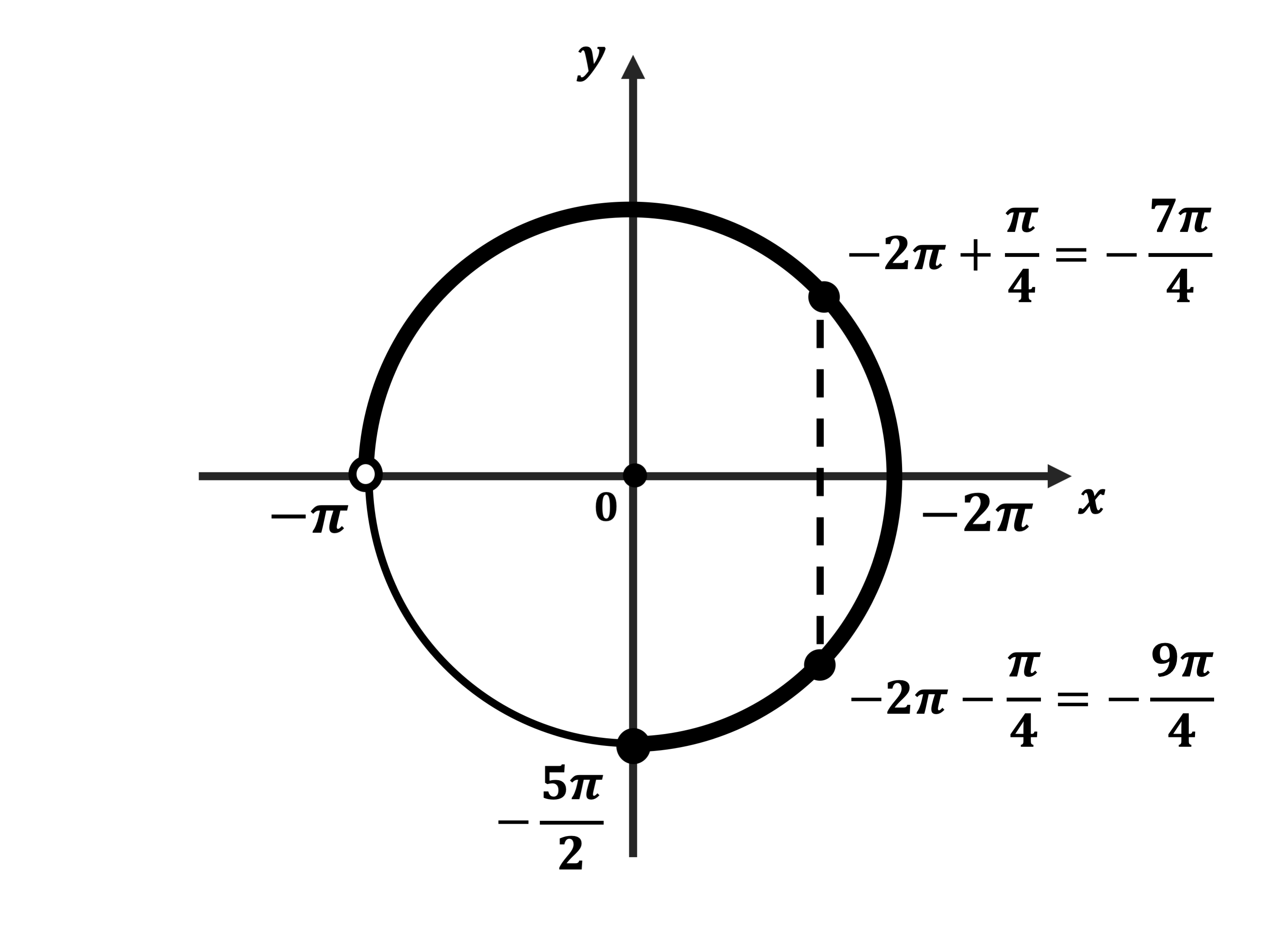
$x_1=-2π+{π}/{4}=-{7π}/{4}$
$x_2=-2π-{π}/{4}=-{9π}/{4}$
Задача 13
а) Решите уравнение ${sin 2x}/{cos(π + x)}= -√2$.
б) Укажите корни этого уравнения, принадлежащие промежутку $(-2π;-{π}/{2})$.
Решение
а)${sin2x}/{cos(π + x)}=-√2$.
Зная, что $sin2x = 2sinxcosx, cos(π + x)=-cosx$, получим: ${2sinxcosx}/{-cosx}=-√2$.
Учитывая, что $cosx≠0, x≠{π}/{2} + πm, m∈Z$, имеем:
$2sinx=√2$,
$sinx = {√2}/{2}$,
$x = {π}/{4} + 2πn, n∈Z$;
$x = {3π}/{4} + 2πk, k∈Z$.
б) Отберём корни уравнения, принадлежащие промежутку $(-2π;-{π}/{2})$.
1. $x = {π}/{4} + 2πn, n∈Z$.
$-2π < {π}/{4} + 2πn < -{π}/{2},$
$-2 < {1}/{4} + 2n < -{1}/{2},$
$-2-{1}/{4} < 2n < -{1}/{2}-{1}/{4},$
$-{9}/{4} < 2n < -{3}/{4},$
$-{9}/{8} < n < -{3}/{8},$
$n = -1$.
При $n =-1$
$x = {π}/{4}-2π=-{7π}/{4}$.
2. $x = {3π}/{4} + 2πk, k∈Z$.
$-2π < {3π}/{4} + 2πk < -{π}/{2}$,
$-2 < {3}/{4} + 2k < -{1}/{2}$,
$-2-{3}/{4} < 2k < -{1}/{2}-{3}/{4}$,
$-{11}/{4} < 2k < -{5}/{4}$,
$-{11}/{8} < k < -{5}/{8}$,
$k = -1$.
При $k = -1$
$x = {3π}/{4}-2π = -{5π}/{4}$.
Задача 14
а) Решите уравнение $9·3^{2 cos x} — 10√3·3^{cos x} + 3 = 0$.
б) Укажите корни этого уравнения, принадлежащие отрезку $[{3π}/{2};4π]$.
Решение
а) После замены $t = 3^{cosx}$ исходное уравнение примет вид $9t^2 — 10√3t + 3 = 0$. Корни этого уравнения $t = √3; t = {√3}/{9}$. Возвращаясь к переменной $x$, получим
$[table3^{cosx}=√3; 3^{cosx}={√3}/{9};$ $[table3^{cosx}=3^{{1}/{2}}; 3^{cosx}=3^{-{3}/{2}};$ $[tablecosx={1}/{2}; cosx=-{3}/{2};$
Второе уравнение совокупности не имеет корней. Решая первое уравнение, получим $x =±{π}/{3} + 2πn; n ∈ Z$.
б) Запишем решение уравнения в виде $x =-{π}/{3} + 2πn; n ∈ Z$ или $x ={π}/{3} + 2πk; k ∈ Z$ и выясним, для каких целых значений $n$ и $k$ справедливы неравенства ${3π}/{2}≤-{π}/{3}+2πn≤4π$ и ${3π}/{2}≤{π}/{3}+2πk≤4π$.
Получим ${11}/{12} ≤ n ≤ {26}/{12}$ и ${7}/{12} ≤ k ≤{22}/{12}$.
Откуда следует, что два целых значения $n = 1$ и $n = 2$ удовлетворяют неравенству ${11}/{12} ≤ n ≤ {26}/{12}; k = 1$ — единственное целое $k$, удовлетворяющее неравенству ${7}/{12} ≤ k ≤{22}/{12}$.
При $n = 1$ $x = -{π}/{3} + 2π·1 = {5π}/{3}$.
При $n = 2$ $x = -{π}/{3} + 2π·2 = {11π}/{3}$.
При $k = 1$ $x = {π}/{3} + 2π·1 = {7π}/{3}$. Итак, ${5π}/{3}; {7π}/{3}; {11π}/{3}$ — корни уравнения, принадлежащие промежутку $[{3π}/{2};4π]$.
Задача 15
а) Решите уравнение $log_2^2(2 sin x + 1) — 17 log_2(2 sin x + 1) + 16 = 0$.
б) Укажите корни этого уравнения, принадлежащие отрезку $[{π}/{4};2π]$.
Решение
а) После замены $t = log_2(2 sin x+1)$ исходное уравнение примет вид $t^2-17t+16 = 0$. Корни этого уравнения $t = 1, t = 16$. Возвращаясь к переменной $x$, получим:
$[tablelog_2(2 sin x + 1) = 1; log_2(2 sin x + 1) = 16;$ $[table2 sin x + 1 = 2;; 2sin x + 1 = 2^{16};$
Второе уравнение совокупности не имеет корней. Решая первое уравнение, получим: $sin x = {1}/{2}; x = (-1)^n{π}/{6} + πn; n ∈ Z$.
б) Запишем решение уравнения в виде $x = {π}/{6} + 2πn; n ∈ Z$ или $x = {5π}/{6} + 2πk; k ∈ Z$ и выясним, для каких целых значений $n$ и $k$ справедливы неравенства ${π}/{4}≤{π}/{6}+2πn≤2π$ и ${π}/{4}≤{5π}/{6}+2πk≤2π$.
Получим: ${1}/{24}≤n≤{11}/{12}$ и $-{7}/{24}≤k≤{7}/{12}$, откуда следует, что нет целых значений $n$, удовлетворяющих неравенству ${1}/{24}≤n≤{11}/{12}; k = 0$ — единственное целое $k$, удовлетворяющее неравенству $-{7}/{24}≤k≤{7}/{12}$.
При $k = 0$ $x = {5π}/{6} + 2π·0 = {5π}/{6}$. Итак, ${5π}/{6}$ — корень уравнения, принадлежащий отрезку $[{π}/{4};2π]$.
Задача 16
а) Решите уравнение $6 log_2^2(2 cos x) — 9 log_2(2 cos x) + 3 = 0$.
б) Найдите все корни этого уравнения, принадлежащие отрезку $[-{π}/{2};π]$.
Решение
а) Решим уравнение $6log_2^2(2 cos x)-9 log_2(2 cos x)+3 = 0$. Обозначим $log_2(2 cos x) = t$ и решим получившееся квадратное уравнение.
$6t^2 — 9t + 3 = 0, t = {9±3}/{12}; t_1 = {1}/{2}; t_2 = 1$.
$[tablelog_2(2 cos x) ={1}/{2}; log_2(2 cos x) = 1;$ $[table2 cos x = √2; 2 cos x = 2;$
$[tablecos x = {√2}/{2}; cos x= 1;$ $[tablex = ±{π}/{4}+ 2π n; n ∊ Z; x = 2πk; k ∊ Z;$
б) Корни, принадлежащие отрезку $[-{π}/{2};π]$, найдём с помощью числовой окружности:
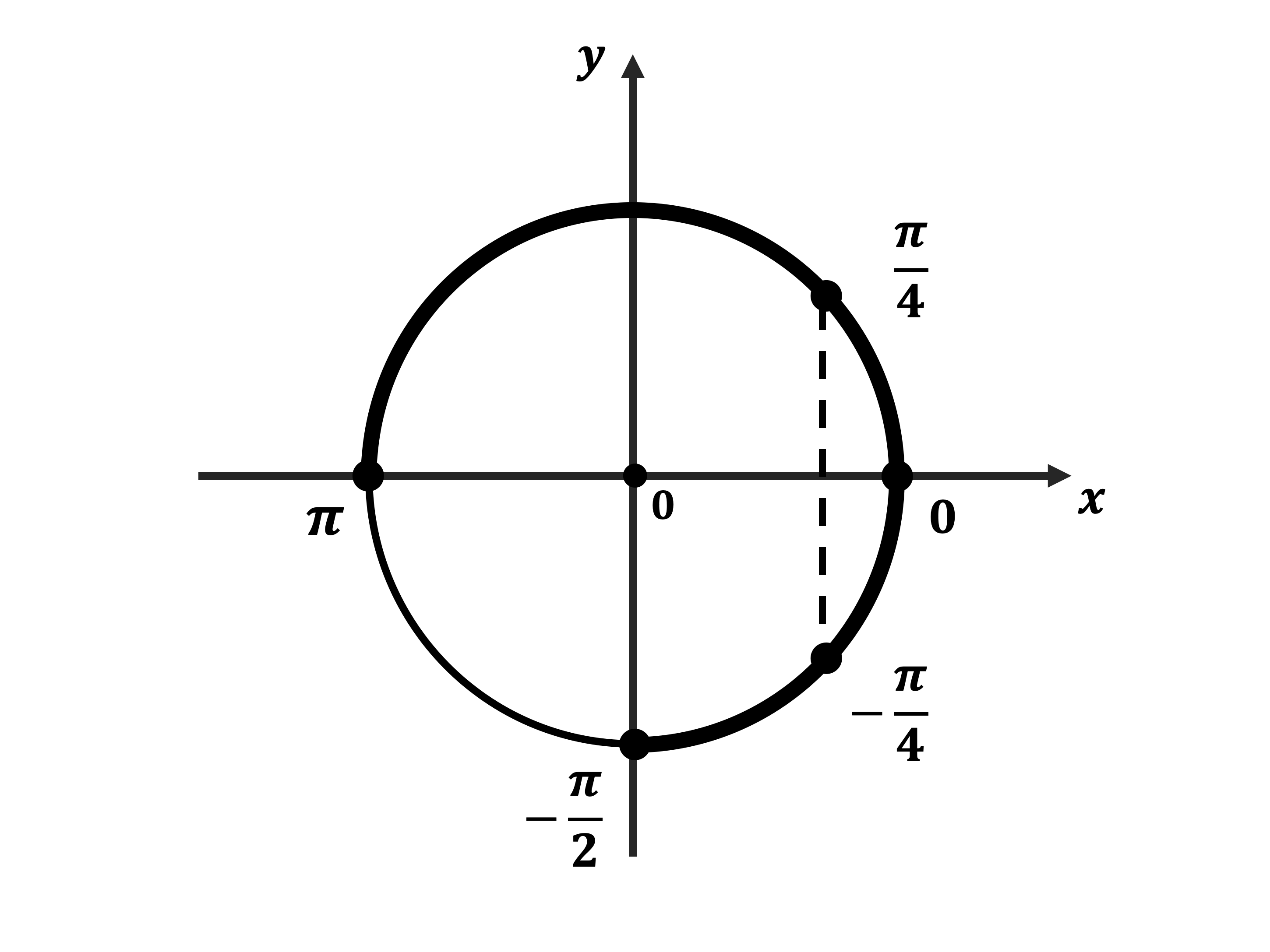
$x_1 = -{π}/{4}; x_2 = 0; x_3 ={π}/{4}$.
Задача 17
а) Решите уравнение $2log_2^2(2 sin x) — 3 log_2(2 sin x) + 1 = 0$.
б) Найдите все корни этого уравнения, принадлежащие отрезку $[{3π}/{2}; 3π]$.
Решение
а) Решим уравнение $2log_2^2(2 sin x) — 3 log_2(2 sin x) + 1 = 0$. Обозначим $log_2(2 sin x) = t$ и решим получившееся уравнение. $2t^2 — 3t + 1 = 0, t = {3±1}/{4}; t_1 = 1; t_2 ={1}/{2}$
$[tablelog_2(2 sin x) = 1; log_2(2 sin x) ={1}/{2};$ $[table2 sin x = 2; 2 sin x=√2;$
$[tablesin x = 1; sin x = {√2}/{2};$ $[tablex={π}/{2}+2πn; x=(-1)^k{π}/{4}+πk;$ $n,k∈Z$
б) Корни, принадлежащие отрезку $[{3π}/{2}; 3π]$, найдём с помощью числовой окружности:
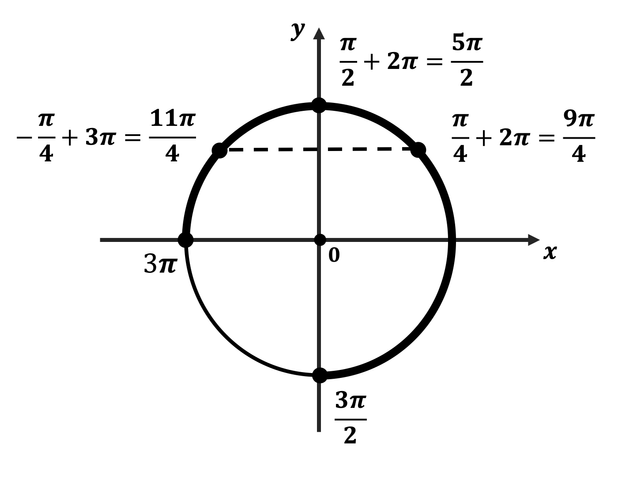
$x_1 = 2π + {π}/{4} = {9π}/{4}; x_2 = 2π + {π}/{2} ={5π}/{2}; x_3 = 3π -{π}/{4} = {11π}/{4}$.
Задача 18
а) Решите уравнение $27^{x} — 5·9^{x} — 3^{x+4} + 405 = 0$.
б) Укажите все корни этого уравнения, принадлежащие отрезку $[log_{3}6; log_{3}10]$.
Решение
а) Преобразуем исходное уравнение и разложим на множители его левую часть.
$3^{3x} — 5·3^{2x} — 81·3^x + 405 = 0$,
$3^{2x}(3^x — 5) — 81(3^x — 5) = 0$,
$(3^{2x} — 81)(3^x — 5) = 0$.
Получаем: $3^{2x} -81 = 0$ или $3^x -5 = 0$. Значит, $3^{2x} = 81$, откуда $x = 2$ или $3^x = 5$, откуда $x = log_{3}5$.
б) Нам нужно выбрать те корни уравнения, которые принадлежат отрезку $[log_{3}6; log_{3}10]$. Заметим, что $2 = log_{3}9$. Тогда $log_{3}5 < log_{3}6 < 2 < log_{3}10$. Значит, указанному отрезку принадлежит корень $x = 2$.
Задача 19
а) Решите уравнение $3√{2}sin({π}/{2}+x)-2=2cos^{2}x$.
б) Укажите корни этого уравнения, принадлежащие отрезку $[{3π}/{2};{5π}/{2}]$.
Решение
а) Запишем исходное уравнение в виде $2 cos^2 x — 3√2 cos x + 2 = 0$.
Решая это уравнение как квадратное относительно $cos x$, получим $(cos x)_{1,2} ={3√2±√{18 — 16}}/{4}={3√2± √2}/{4}$.
Значит, $(cos x)_1 = {√2}/{2}$, откуда $x =π/4 + 2πn, n ∈ Z$ или $x =-π/4 + 2πn, n ∈ Z$.
Уравнение $(cosx)_2 = √2$ корней не имеет.
б) Отберём корни, принадлежащие отрезку $[{3π}/{2};{5π}/{2}]$ с помощью числовой окружности.
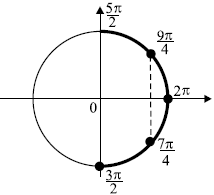
Получим числа
$2π -{π}/{4} ={7π}/{4}$;
$2π + {π}/{4} = {9π}/{4}$.
Задача 20
а) Решите уравнение $3√{3}cos({3π}/{2}+x)-3=2sin^{2}x$.
б) Укажите корни этого уравнения, принадлежащие отрезку $[2π; 3π]$.
Решение
а) Запишем исходное уравнение в виде $2sin^2 x — 3√3 sin x + 3 = 0$.
Решая это уравнение как квадратное относительно $sin x$, получим $(sin x)_{1,2} = {3√3±√{27-24}}/{4}= {3√3±√3}/{4}$.
Значит,$(sin x)_1 ={√3}/{2}$, откуда $x ={π}/{3} +2πn, n ∈ Z$ или $x ={2π}/{3}+2πm, m ∈ Z$.
Уравнение $(sin x)_2 = √3$ корней не имеет.
б) С помощью числовой окружности отберём корни, принадлежащие отрезку: $[2π; 3π]$
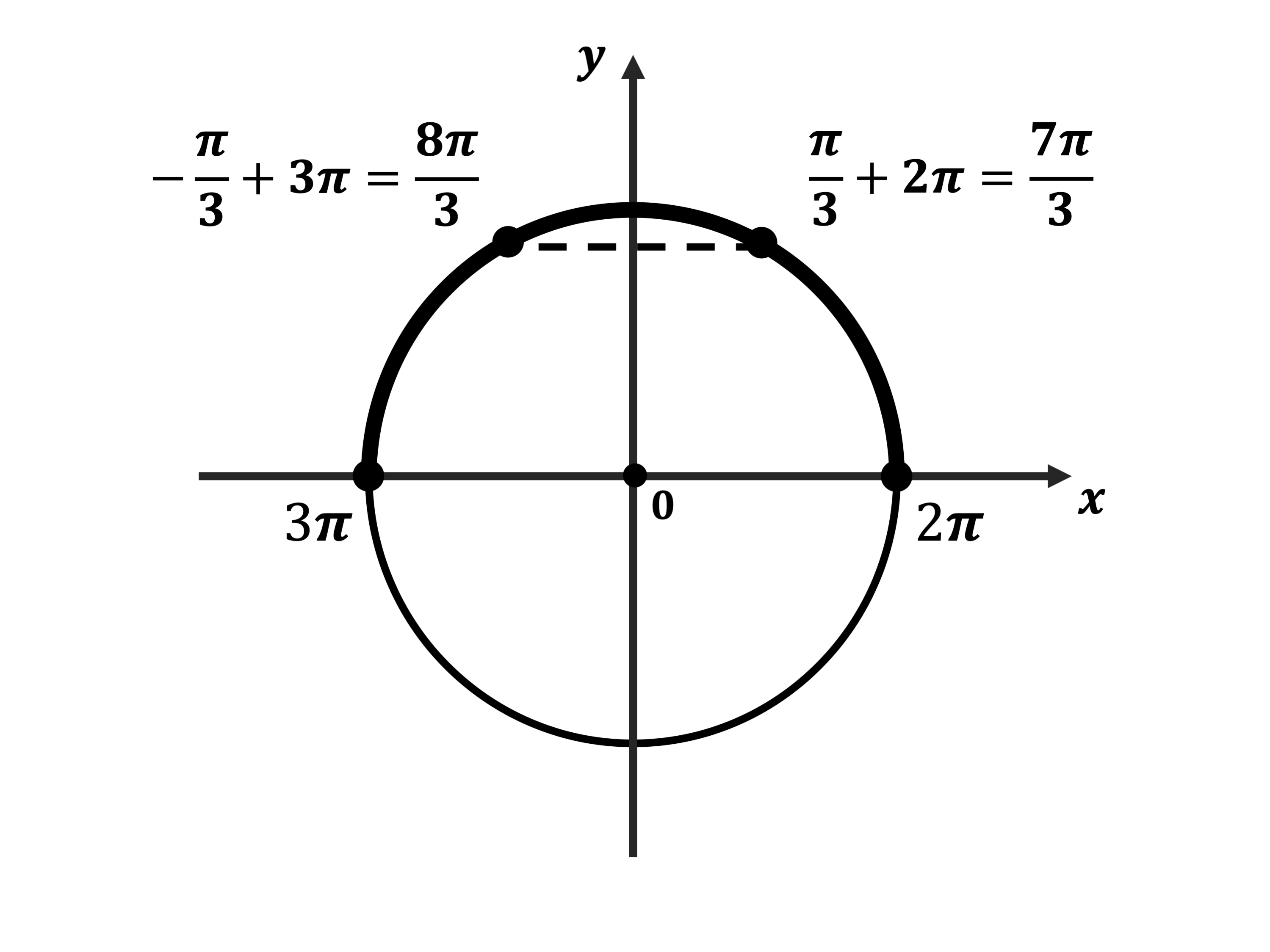
Получим числа:
$2π +{π}/{3}={7π}/{3}$;
$3π -{π}/{3}={8π}/{3}$.