Задание 15. Алгебра логики. Преобразование и анализ логических выражений. ЕГЭ 2024 по информатике
Средний процент выполнения: 68.7%
Ответом к заданию 15 по информатике может быть цифра (число) или слово.
Задачи для практики
Задача 1
На числовой прямой даны два отрезка: P = [18, 63] и Q = [2, 29]. Укажите наименьшую возможную длину такого отрезка A, что логическое выражение
$ (¬(x ∈ A) → ((x ∈ P) ∧ (x ∈ A))) ∨ ((x ∈ Q) → (x ∈ P))$
тождественно истинно, то есть принимает значение 1 при любом значении переменной x.
Решение
1) преобразуем выражение, заменив (x∈A) на А, (x∈P) на P,(x∈Q) на Q
(A / P*A) / ¬Q / P
первую скобку преобразуем по формуле поглощения
A / ¬Q / P
2) Строим числовую прямую и отмечаем на ней значения известной части (¬Q / P)
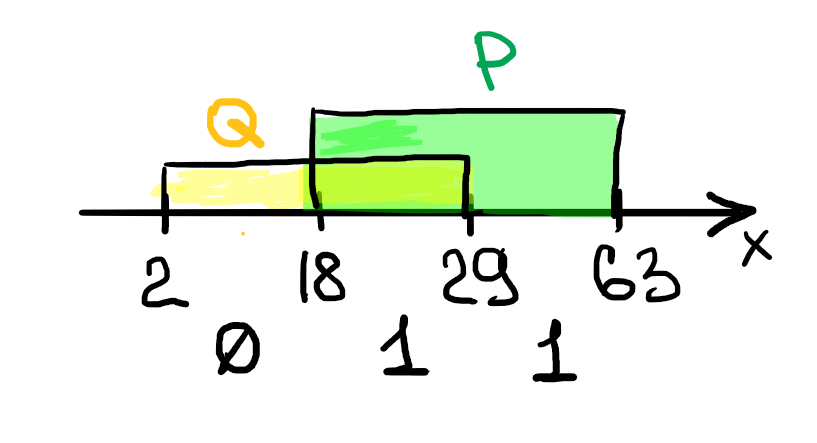
3) Чтобы выражение было истинным на всей числовой оси, необходимо и достаточно, чтобы A ∈ [2, 18], поскольку на этом отрезке известная часть ложна. Длина отрезка = 16
Задача 2
Даны множества P = {5, 8, 19, 24, 42, 124}, Q = {3, 8, 12, 24, 64, 127, 211} и A. Элементами множества являются натуральные числа. Известно, что выражение
((x ∈ A) → ¬((x ∈ P) ∨ (x ∈ A))) ∨ ¬((x ∈ Q) → ¬(x ∈ P)).
истинно (т. е. принимает значение 1) при любом значении переменной x. Определите наибольшее возможное значение суммы элементов множества A.
Решение
Обозначим $P↖{∼}$: (x ∈ P); $Q↖{∼}$: (x ∈ Q); $A↖{∼}$: (x ∈ A).
Перепишем исходное выражение: ($A↖{∼}$ → ¬($P↖{∼}$ ∨ $A↖{∼}$)) ∨ ¬($Q↖{∼}$ → ¬ $P↖{∼}$).
На основании законов алгебры логики преобразуем это выражение.
($A↖{∼}$ → ¬($P↖{∼}$ ∨ $A↖{∼}$)) ∨ ¬($Q↖{∼}$ → ¬ $P↖{∼}$) ≡
≡ (¬ $A↖{∼}$ ∨ ¬($P↖{∼}$ ∨ $A↖{∼}$)) ∨ ¬(¬$Q↖{∼}$ ∨ ¬ $P↖{∼}$) ≡
≡ ¬ $A↖{∼}$ ∨ (¬ $P↖{∼}$ ∧ ¬ $A↖{∼}$) ∨ ($Q↖{∼}$ ∧ $P↖{∼}$) ≡
≡ ¬ $A↖{∼}$ ∨ ($Q↖{∼}$ ∧ $P↖{∼}$)
Возвращаясь к исходным выражениям, получим: ((x ∉ A) ∨ ((x ∈ Q)) ∧ (x ∈ P)).
Логическое выражение (x ∈ Q)) ∧ (x ∈ P) истинно на промежутке на множестве Q ∩ P = {8, 24}. Согласно условию, нужно выбрать такое множество A, что для любого целого x будет истинным выражение (x ∉ A) ∨ x ∈ {8, 24}. При этом множество A должно содержать наибольшее число элементов.
Таким множеством A является {8, 24}.Сумма элементов этого множества равна 32.
Задача 3
На числовой прямой даны два отрезка: P = [1, 70] и Q = [25, 96]. Укажите наибольшую возможную длину такого отрезка A, что логическое выражение
((x ∈ P) → ((x ∈ Q) ∧ (x ∈ P))) → ¬(x ∈ A)
тождественно истинно, то есть принимает значение 1 при любом значении переменной x.
Решение
Преобразуем выражение:
((x ∈ P) → ((x ∈ Q) ∧ (x ∈ P))) → ¬(x ∈ A) преобразуем импликацию
(¬(x ∈ P) / ((x ∈ Q) ∧ (x ∈ P))) → ¬(x ∈ A) применяем формулу поглощения
(¬(x ∈ P) / (x ∈ Q)) → ¬(x ∈ A) преобразуем импликацию
(x ∈ P) / ¬(x ∈ Q) / ¬(x ∈ A)
Известная часть: (x ∈ P) / ¬(x ∈ Q) истинна на отрезке от 1 до 25.
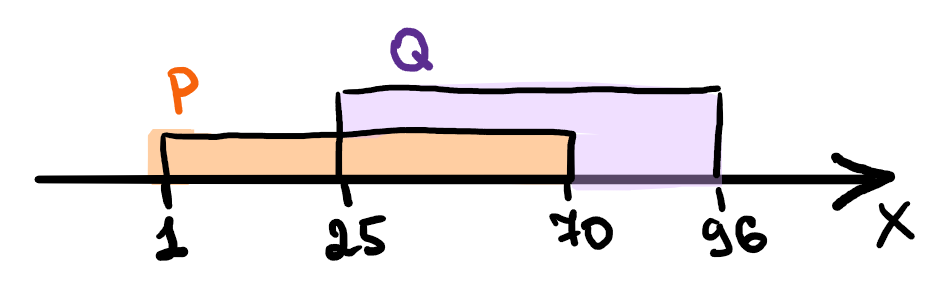
Чтобы выражение было истинно на всей числовой прямой, необходимо чтобы ¬(x ∈ A) было истинно, поэтому отрезок не должен лежать вне границ отрезка [1, 25], то есть А ∈ [1, 25] и его длина 25 — 1 = 24
Задача 4
На числовой прямой даны два отрезка: P = [2, 35] и Q = [12, 54]. Укажите наибольшую возможную длину такого отрезка A, что логическое выражение
$ ((x ∈ P) → ((x ∈ Q) ∧ (x ∈ P))) → ¬(x ∈ A)$
тождественно истинно, то есть принимает значение 1 при любом значении переменной x.
Решение
Задача 5
Для какого наименьшего целого числа A выражение
$((x^4 < A) → (x ≤ 2)) ∧ ((y < 7) → (y^2 < A))$
тождественно истинно (то есть принимает значение 1 при любых целых неотрицательных значениях переменных x и y)?
Решение
Задача 6
Для какого наибольшего целого числа A выражение
$((x ≤ 6) → (x^2 ≤ A)) ∧ ((y^3 ≤ A) → (y ≤ 3))$
тождественно истинно (то есть принимает значение 1 при любых целых неотрицательных значениях переменных x и y)?
Решение
Задача 7
Для какого наименьшего целого числа A выражение
$((x · x < A) ∨ (x ≥ 8)) ∧ ((y · y < A) → (y < 8))$
тождественно истинно (то есть принимает значение 1 при любых целых неотрицательных значениях переменных x и y)?
Решение
Задача 8
Для какого наибольшего целого неотрицательно числа A выражение
$(4 · x + 8 · y ≠ 124) ∨ (x > 3 · A − 1) ∨ (2 · y > A)$
тождественно истинно (то есть принимает значение 1 при любых целых неотрицательных значениях переменных x и y)?
Решение
Задача 9
Для какого наибольшего целого неотрицательно числа A выражение
(5 · x + 2 · y ≠ 32) ∨ (x > A − 8) ∨ (y > A + 1)
тождественно истинно (то есть принимает значение 1 при любых целых неотрицательных значениях переменных x и y)?
Решение
Задача 10
Для какого наименьшего целого неотрицательно числа A выражение
$(x + 2 · y ≤ A) ∨ (x > 25) ∨ (y > 12)$
тождественно истинно (то есть принимает значение 1 при любых целых неотрицательных значениях переменных x и y)?