- Задание 2. Алгебра логики. Таблицы истинности. ЕГЭ 2024 по информатике
- Задачи для практики
- Задача 1
- Задача 2
- Задача 3
- Задача 4
- Задача 5
- Задача 6
- Задача 7
- Задача 8
- Задача 9
- Задача 10
- Задача 11
- Задача 12
- Теория для 2 задания ЕГЭ по информатике
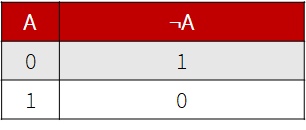
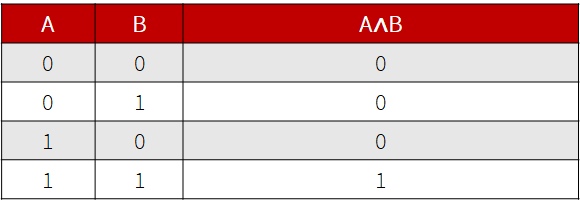
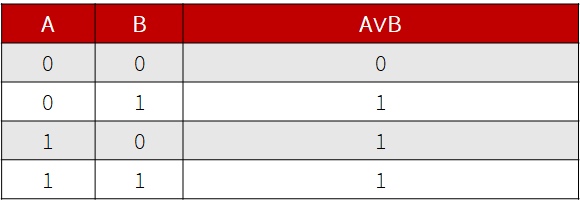
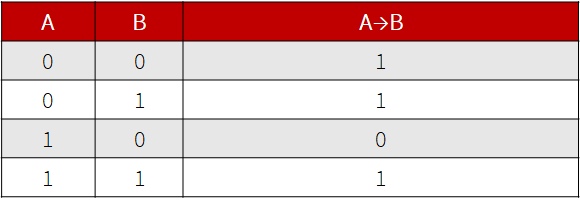
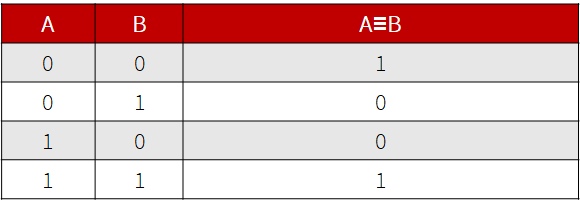
- Основные логические операции
- Порядок логических операций
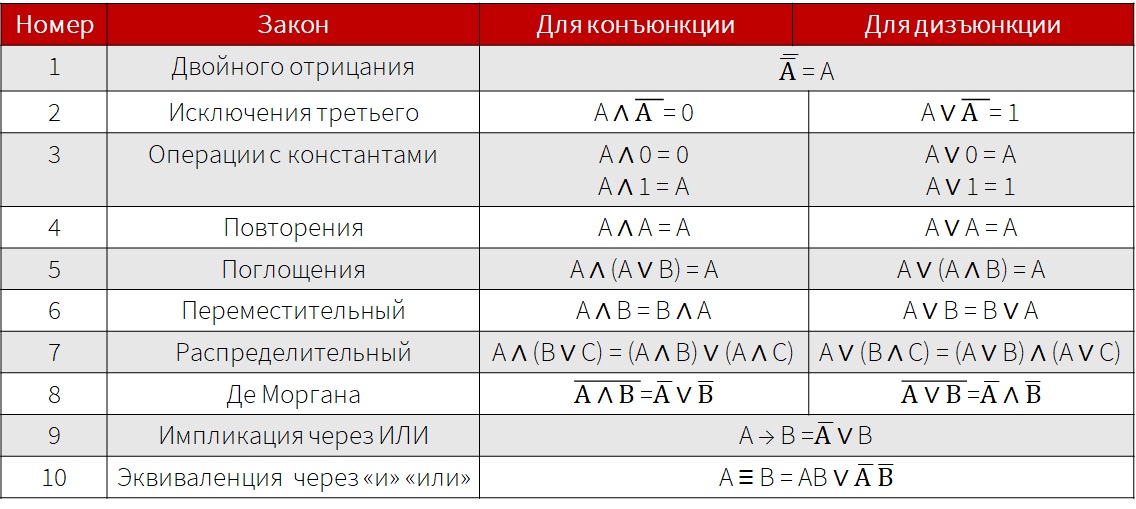
- Законы логики
- Практика
Задание 2. Алгебра логики. Таблицы истинности. ЕГЭ 2024 по информатике
Средний процент выполнения: 65.9%
Ответом к заданию 2 по информатике может быть цифра (число) или слово.
Теория к 2 заданию: читать
Задачи для практики
Задача 1
Дано логическое выражение, зависящее от 6 логических переменных:
¬(A → F) ∧ B ∧ ¬C ∧ (D → E).
Сколько существует различных наборов значений переменных, при которых выражение ложно?
Решение
Заметим, что все скобки и выражения связаны конъюнкцией, для которой сложно получить единицу. Поэтому будет решать от обратного. Посчитаем количество наборов, когда выражение истинно, тогда:
¬(A → F) = 1, тогда $A → F = 0$, следовательно, A = 1, F = 0.
B = 1.
¬C = 1, значит C = 0.
(D → E) = 1, тогда возможно 3 варианта: D = 0, E = 0; D = 0, E = 1; D = 1, E = 1.
Перемножим количество подходящих значений для каждой переменной: A, B, C, F — по одному набору, D и E — 3 набора. Итого:
1 х 3 = 3 набора, для которых вся функция истинна. Но нам нужно, чтобы функция была ложна. Найдём общее количество наборов по формуле $k = 2^N$, где N — количество переменных. У нас 6 переменных, значит всего наборов 64. Из них 3 нам не подходят. Тогда количество подходящих (ложных) наборов:
64 — 3 = 61.
Или при помощи программы на С++:
#include <iostream>
#include <algorithm>
#include <fstream>
using namespace std;
bool f(int A, int B, int C, int D, int E, int F){
return (!(!A || F) && B && !C && (!D || E));
}
int main() {
int count = 0;
for (int A = 0; A <= 1; ++A)
for (int B = 0; B <= 1; ++B)
for (int C = 0; C <= 1; ++C)
for (int D = 0; D <= 1; ++D)
for (int E = 0; E <= 1; ++E)
for (int F = 0; F <= 1; ++F)
if (f(A, B, C, D, E, F) == false)
count++;
cout << count;
return 0;
}
Ответ: 61.
Задача 2
Дано логическое выражение, зависящее от 5 логических переменных:
$(A ∨ ¬B) ∧ (¬C ∨ D ∨ ¬E)$.
Сколько существует различных наборов значений переменных, при которых выражение ложно?
Решение
В первой скобке 2 переменных, значит для неё будет 4 набора. Поскольку переменные соединяются дизъюнкцией, выражение ложно ровно в одном случае, а в трёх оставшихся — истинно.
Во второй скобке 3 переменных, значит для неё будет 8 наборов. Поскольку переменные соединяются дизъюнкцией, выражение ложно ровно в одном случае, а в семи оставшихся — истинно.
Конъюнкция ложна, когда хотя бы одна скобка ложна. Рассмотрим 3 случая:
Первая скобка ложна, вторая истинна. Первая скобка ложна в 1 случае из 4, вторая истинна в 7 случаях из 8. Итого 7 · 1 = 7.
Первая скобка истинна, вторая ложна. Первая скобка истинна в 3 случаях из 4, вторая ложна в 1 случае из 4. Итого 1 · 3 = 3.
Первая скобка ложна, вторая ложна. Первая скобка ложна в 1 случае из 4, вторая ложна в 1 случае из 8. Итого 1 · 1 = 1.
Суммарно: 7 + 3 + 1 = 11.
Ответ: 11.
Задача 3
Дано логическое выражение, зависящее от 5 логических переменных:
(¬A ∧ B ∧ C) ∨ (¬D ∧ ¬E).
Сколько существует различных наборов значений переменных, при которых выражение истинно?
Решение
В первой скобке 3 переменных, значит для неё будет 8 наборов. Поскольку переменные соединяются конъюнкцией, выражение истинно ровно в одном случае, а в семи оставшихся — ложно.
Во второй скобке 2 переменных, значит для неё будет 4 набора. Поскольку переменные соединяются конъюнкцией, выражение истинно ровно в одном случае, а в трёх оставшихся — ложно.
Дизъюнкция истинна, когда хотя бы одна скобка истинна. Рассмотрим 3 случая:
Первая скобка ложна, вторая истинна. Первая скобка ложна в 7 случаях из 8, вторая истинна в 1 случае из 4. Итого 7 · 1 = 7.
Первая скобка истинна, вторая ложна. Первая скобка истинна в 1 случае из 8, вторая ложна в 3 случаях из 4. Итого 1 · 3 = 3.
Первая скобка истинна, вторая истинна. Первая скобка истинна в 1 случае из 8, вторая истинна в 1 случае из 4. Итого 1 · 1 = 1.
Суммарно: 7 + 3 + 1 = 11.
Ответ: 11.
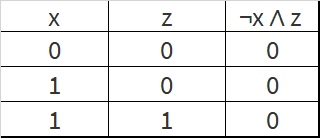
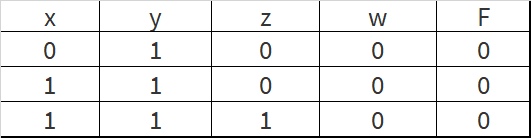
Задача 4
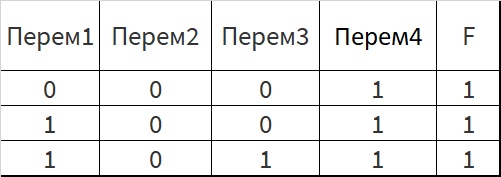
Логическая функция F задаётся выражением ((x∧z)∨¬x)∧¬w∧y. Во фрагменте таблицы истинности приведены все строки, при которых значение функции F является истиной. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
| F | ||||
| 1 | 0 | 0 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 | 1 |
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала букву, соответствующую 1-му столбцу; затем букву, соответствующую 2-му столбцу; затем букву, соответствующую 3-му столбцу; затем букву, соответствующую последнему столбцу). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Решение
Строим таблицу истинности для логической функции любым способом и находим наборы, при которых функция ложна. Например, при помощи программы:
bool f(int x, int y, int z, int w){
return (((x && z) || !x) && !w && y);
}
int main() {
cout << "x y z w F" << endl;
for (int x = 0; x <= 1; ++x)
for (int y = 0; y <= 1; ++y)
for (int z = 0; z <= 1; ++z)
for (int w = 0; w <= 1; ++w)
if (f(x, y, z, w) == true)
cout << x << " " << y << " "
<< z << " " << w << " " << f(x, y, z, w) << endl;
return 0;
}
Получили наборы:
x y z w F
0 1 0 0 1
0 1 1 0 1
1 1 1 0 1
Начинаем сопоставление с исходной тбалицей:
1) столбец без единиц четвёртый в таблице из условия — это W
2) столбец с одной единицей третий в исходной таблице — это X
3) столбей с тремя единицами — это Y
4) столбец с двумя единицами — это Z
Результат: YZXW
Задача 5
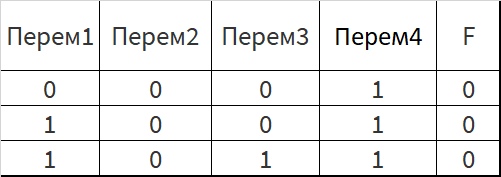
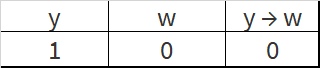
Логическая функция F задаётся выражением (y → w) ∨ (¬x ∧ z). Во фрагменте таблицы истинности приведены все строки, при которых значение функции F ложно. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
| F | ||||
| 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 | 0 |
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала букву, соответствующую 1-му столбцу; затем букву, соответствующую 2-му столбцу; затем букву, соответствующую 3-му столбцу; затем букву, соответствующую последнему столбцу). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Решение
Строим таблицу истинности для логической функции любым способом и находим наборы, при которых функция ложна. Например, при помощи программы:
bool f(int x, int y, int z, int w){
return ((!y || w) || (!x && z));
}
int main() {
cout << "x y z w F" << endl;
for (int x = 0; x <= 1; ++x)
for (int y = 0; y <= 1; ++y)
for (int z = 0; z <= 1; ++z)
for (int w = 0; w <= 1; ++w)
if (f(x, y, z, w) == false)
cout << x << " " << y << " "
<< z << " " << w << " " << f(x, y, z, w) << endl;
return 0;
}
Получили наборы:
x y z w F
0 1 0 0 0
1 1 0 0 0
1 1 1 0 0
Начинаем сопоставление с исходной тбалицей:
1) столбец без единиц второй в таблице из условия — это W
2) столбец с одной единицей третий в исходной таблице — это Z
3) столбей с тремя единицами — это Y
4) столбец с двумя единицами — это X
Результат: xwzy
Задача 6
Дан фрагмент таблицы истинности выражения F:
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | F |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
Сколько строк таблицы удовлетворяют выражению: F = (x1 ∨ x2 ∨ x3) ∧ x4 ∧ (x5 ∨ x6 ∨ x7) ∧ x8?
Решение
Данное выражение является конъюнкцией четырёх выражений. Конъюнкция нескольких высказываний истинна тогда и только тогда, когда истинными являются все входящие в неё высказывания. Следовательно, x4 = 1, x8 = 1 и в наборах значений переменных (x1, x2, x3), (x5, x6, x7) должна быть хотя бы одна 1.
Этим условиям удовлетворяют три последние строки таблицы. В каждой из этих строк значение функции F = 1. Следовательно, эти строки удовлетворяют заданному логическому выражению.
Чтобы остальные строки удовлетворяли заданному выражению, значение F должно быть равно 0. В таблице количество таких строк равно 5.
Всего значения 8 строк таблицы удовлетворяют заданному выражению.
Задача 7
Логическая функция F задаётся выражением (¬x → y) ∧ (z → y). Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.
| Переменная 1 ??? |
Переменная 2 ??? |
Переменная 3 ??? |
Функция F |
| 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 |
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая 1-му столбцу; затем — буква, соответствующая 2-му столбцу; затем — буква, соответствующая 3-му столбцу). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x ∨ ¬y, зависящее от двух переменных x и y, и таблица истинности:
| Переменная 1 ??? |
Переменная 2 ??? |
Функция F |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
Тогда 1-му столбцу соответствует переменная y, а 2-му столбцу соответствует переменная x. В ответе нужно написать: yx.
Решение
Преобразуем исходное выражение.
(¬x → y) ∧ (z → y) = (x ∨ y) ∧ (¬z ∨ y) = y ∨ (x ∧ ¬z).
Так как дизъюнкция ложна только в том случае, когда ложны оба высказывания, входящие в неё, то переменной y должен соответствовать тот столбец, в котором значение 0 стоит в тех же строках, что и в столбце F. Следовательно, переменной y соответствует третий столбец.
Рассмотрим строку, в которой значение функции отличается от значения переменной y. Такой строкой является четвёртая снизу. Здесь переменная y = 0, а значение функции F = 1. Это означает, что x ∧ ¬z = 1. В рассматриваемой строке значение первого столбца 0, а второго 1. Пусть x = 0, z = 1. При этих значениях логическое выражение x ∧ ¬z ложно, что не соответствует табличному значению функции F = 1. Следовательно, x = 1, z = 0. Значит, первый столбец соответствует переменной z, а второй—x.
Или при помощи программы на С++:
Выводим только ложные наборы, потому что их меньше
#include <iostream>
#include <algorithm>
#include <fstream>
using namespace std;
bool f(int x, int y, int z){
return ((x || y) && (!z || y));
}
int main() {
cout << "x y z F" << endl;
for (int x = 0; x <= 1; ++x)
for (int y = 0; y <= 1; ++y)
for (int z = 0; z <= 1; ++z)
if (f(x, y, z) == false)
cout << x << " " << y << " "
<< z << " " << f(x, y, z) << endl;
return 0;
}
Задача 8
Логическая функция F задаётся выражением ((¬z∨¬x)∧z)∨w∨¬y. Во фрагменте таблицы истинности приведены все строки, при которых значение функции F ложно. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
| F | ||||
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 |
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала букву, соответствующую 1-му столбцу; затем букву, соответствующую 2-му столбцу; затем букву, соответствующую 3-му столбцу; затем букву, соответствующую последнему столбцу). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x∨¬y, зависящее от двух переменных x и y, и таблица истинности
| F | ||
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
тогда 1-му столбцу соответствует переменная y, а 2-му столбцу соответствует переменная x. В ответе нужно написать: yx.
Решение
Задача 9
Логическая функция F задаётся выражением (y ∧ (w → x)) → g. Во фрагменте таблицы истинности приведены все строки, при которых значение функции F ложно. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, w, g.
| F | ||||
| 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 | 0 |
В ответе напишите буквы x, y, w, g в том порядке, в котором идут соответствующие им столбцы (сначала букву, соответствующую 1-му столбцу; затем букву, соответствующую 2-му столбцу; затем букву, соответствующую 3-му столбцу; затем букву, соответствующую последнему столбцу). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x∨¬y, зависящее от двух переменных x и y, и таблица истинности
| F | ||
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
тогда 1-му столбцу соответствует переменная y, а 2-му столбцу соответствует переменная x. В ответе нужно написать: yx.
Решение
Задача 10
Логическая функция F задаётся выражением (x → y) → (w → g). Во фрагменте таблицы истинности приведены все строки, при которых значение функции F ложно. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, w, g.
| F | ||||
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
В ответе напишите буквы x, y, w, g в том порядке, в котором идут соответствующие им столбцы (сначала букву, соответствующую 1-му столбцу; затем букву, соответствующую 2-му столбцу; затем букву, соответствующую 3-му столбцу; затем букву, соответствующую последнему столбцу). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x∨¬y, зависящее от двух переменных x и y, и таблица истинности
| F | ||
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
тогда 1-му столбцу соответствует переменная y, а 2-му столбцу соответствует переменная x. В ответе нужно написать: yx.
Решение
Задача 11
Логическая функция F задаётся выражением (x = y) ∨ ¬(y → w) ∨ z. Ниже приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z.
| F | ||||
| 1 | 1 | 0 | 0 | |
| 1 | 1 | 0 | ||
| 0 | 1 | 0 |
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала букву, соответствующую 1-му столбцу; затем букву, соответствующую 2-му столбцу; затем букву, соответствующую 3-му столбцу; затем букву, соответствующую последнему столбцу). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Если бы функция F была задана выражением x ∨ ¬y, зависящим от двух переменных x и y, а фрагмент таблицы истинности имел бы вид:
| F | ||
| 1 | 0 | 0 |
тогда 1-му столбцу соответствовала бы переменная y, а 2-му столбцу — переменная x. В ответе следовало бы написать: yx.
Решение
Задача 12
Логическая функция F задаётся выражением (x = y)∨(x∧w)∨¬z. Ниже приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z.
| F | ||||
| 1 | 0 | 0 | ||
| 0 | 0 | 0 | ||
| 0 | 1 | 0 |
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала букву, соответствующую 1-му столбцу; затем букву, соответствующую 2-му столбцу; затем букву, соответствующую 3-му столбцу; затем букву, соответствующую последнему столбцу). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Если бы функция F была задана выражением x ∨ ¬y, зависящим от двух переменных x и y, а фрагмент таблицы истинности имел бы вид:
| F | ||
| 1 | 0 | 0 |
тогда 1-му столбцу соответствовала бы переменная y, а 2-му столбцу — переменная x. В ответе следовало бы написать: yx.
Решение
Теория для 2 задания ЕГЭ по информатике
Основная тема задания №2 — алгебра логики. С неё и начнём. Для успешного решения номера вам важно знать 3 теоретических момента:
- Основные логические операции
-
Порядок логических операций
-
Законы логики
Основные логические операции
1. Инверсия «НЕ»
Логическое отрицание
Обозначения: ¬А, Ā
Меняет значение на противоположное
2. Конъюнкция «И»
Логическое умножение
Обозначения: А∧В, А & В, А и В, AB
Принимает значение «истина», когда все значения единицы.
Хотя бы один 0 обнуляет всё.
3. Дизъюнкция «ИЛИ»
Логическое сложение
Обозначения: А∨В, А | В, А или В
Принимает значение «истина», когда хотя бы одна единица. «Ложь», когда все нули.
4. Импликация «Если, то»
Следование
Обозначения: А→В, А => В
Из истины следует истина, из лжи что угодно
5. Эквивалентность «Равны»
Тождество
Обозначения: А≡В, А <=> В
Иcтина, когда значения одинаковы. Ложь, когда различны
Порядок логических операций
- Действия в скобках
- Инверсия
- Конъюнкция
- Дизъюнкция
- Импликация
- Эквивалентность
Законы логики
Законов логики существует огромное количество, но именно для ЕГЭ достаточно знать 10 законов из данной таблицы. Некоторые из них очевидные, некоторые придётся выучить.
Практика
Основных вариантов решения два: логические рассуждения, либо построение таблицы истинности. Иногда проще решать первым методом, иногда вторым.
Первый метод. Логические рассуждения.
Пример:
Логическая функция F задаётся выражением y ∧ (x → z) ∧ ¬w. Во фрагменте таблицы истинности приведены все строки, при которых значение функции F истинно.Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
Решение:
Итоговая функция всегда истинна для нашей таблицы (единички в значениях F). Заметим, что в последнюю очередь выполняются две конъюнкции, значение которых будет = 1 только тогда, когда значение каждого выражение равно 1.
Вывод:
y = 1
(x → z) = 1
¬w = 1,а значит w = 0
y всегда 1, такой столбик лишь один: y — переменная 4
w всегда 0, такой столбик лишь один: w — переменная 2
Для x и z остаётся переменная 1 и переменная 3. Осталось определится с порядком.
(x → z) = 1, значит не может быть набора, когда x = 1, а z = 0.
Во второй строчке перем1 = 1, а перем3 = 0. Следовательно, z — переменная 1, x — переменная 3.
z — переменная 1
w — переменная 2
x — переменная 3
y — переменная 4
Ответ: zwxy
Второй метод. Таблица истинности
Пример:
Логическая функция F задаётся выражением (y → w) ∨ (¬x ∧ z). Во фрагменте таблицы истинности приведены все строки, при которых значение функции F ложно. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
Решение:
Итоговая функция всегда равна нулю. Между скобками дизъюнкция, значит обе скобки должны быть ложными. Рассмотрим каждую скобку отдельно:
y → w = 0
¬x ∧ z = 0
Объединяем все переменные в одну таблицу:
Соотносим её с таблицей из условия:
y — переменная 4
w — переменная 2
x — переменная 1
z — переменная 3
Ответ: xwzy