Задание 13. Графы. Количество путей. ЕГЭ 2024 по информатике
Средний процент выполнения: 60.5%
Ответом к заданию 13 по информатике может быть цифра (число) или слово.
Задачи для практики
Задача 1
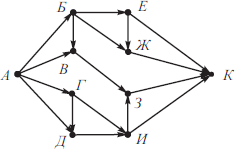
На рисунке изображена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?
Решение
Построим таблицу. В первую строку таблицы запишем наименование всех вершин в следующем порядке. Сначала запишем вершину К. Затем те вершины, из которых в К ведёт прямой путь и из которых в вершину К можно попасть только через уже просмотренные вершины. Далее вершины, из которых в уже просмотренные вершины ведёт прямой путь и из которых можно попасть только через уже просмотренные вершины. Получим:
| К | З | И | Ж | Е | В | Б | Д | Г | А |
Вторую строку таблицы заполним числами, соответствующими количеству исходящих путей Px(K) из просматриваемой вершины x в K. Если из вершины x выходит несколько путей, например, в вершины x1, x2, и x3, то количество путей, ведущих из этой вершины в К, будет равно сумме путей, ведущих из x1, x2, и x3 в К.
То есть Px(K) = Px1 (K) + Px2 (K) + Px3 (K).
Для вершины К в таблицу заносим значение PК(K) = 1.
Следующей идёт вершина З. Из этой вершины выходит путь только в одну вершину К. PЗ(K) = PК(K) = 1.
Из вершины И выходят два пути в вершины З и К.
PИ(K) = PЗ(K) + PК(K) = 1 + 1 = 2.
Из вершины Ж выходит путь только в одну вершину К.
PЖ(K) = PК(K) = 1.
Из вершины Е выходят два пути в вершины Ж и К.
PЕ(K) = PЖ(K) + PК(K) = 1 + 1 = 2.
Из вершины В выходит путь только в одну вершину З.
PВ(K) = PЗ(K) = 1.
Из вершины Б выходят пути в вершины Е, Ж и В. Следовательно, PБ(K) = PЕ(K) + PЖ(K) + PВ(K) = 2 + 1 + 1 = 4.
Из вершины Д выходит путь только в одну вершину И.
PД(K) = PИ(K) = 2.
Из вершины Г выходят два пути в вершины И и Д.
PГ(K) = PД(K) + PИ(K) = 2 + 2 = 4.
Из вершины А выходят пути в вершины Б, В, Г и Д. Следовательно, PА(K) = PБ(K) + PВ(K) + PГ(K) + PД(K) = 4 + 1 + 4 + 2 = 11.
Получим:
| К | З | И | Ж | Е | В | Б | Д | Г | А |
| 1 | 1 | 2 | 1 | 2 | 1 | 4 | 2 | 4 | 11 |
Задача 2
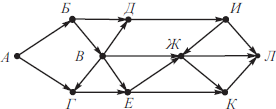
На рисунке изображена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Л, не проходящих через пункт Ж?
Решение
Построим таблицу. В первую строку таблицы запишем наименование всех вершин в следующем порядке. Сначала запишем вершину Л. Затем те вершины, из которых в Л ведёт прямой путь и из которых в вершину Л можно попасть только через уже просмотренные вершины. Далее вершины, из которых в уже просмотренные вершины ведёт прямой путь и из которых можно попасть только через уже просмотренные вершины. Получим:
| Л | К | Ж | Е | И | Д | Г | В | Б | А |
Вторую строку таблицы заполним числами, соответствующими количеству исходящих путей Px(Л) из просматриваемой вершины x в Л, не проходящих через пункт Ж. Если из вершины x выходит несколько путей, например, в вершины x1, x2, и x3, то количество путей, ведущих из этой вершины в Л, не проходящих через пункт Ж, будет равно сумме путей, ведущих из x1, x2, и x3 в Л.
То есть Px(Л) = Px1(Л) + Px2 (Л) + Px3(Л).
Для вершины Л в таблицу заносим значение PЛ(Л) = 1.
Следующей идёт вершина К. Из этой вершины выходит путь только в одну вершину Л. PК(Л) = PЛ(Л) = 1.
Следующей в таблице идёт вершина Ж. Так как мы ищем пути, не проходящие через эту вершину, то PЖ(Л) = 0.
Из вершины Е выходят два пути в вершины Ж и К.
PЕ(Л) = PК(Л) + PЖ(Л) = 1 + 0 = 1.
Из вершины И выходят два пути в вершины Л и Ж.
PИ(Л) = PЖ(Л) + PЛ(Л) = 0 + 1 = 1.
Из вершины Д выходит путь только в одну вершину И.
PД(Л) = PИ(Л) = 1.
Из вершины Г выходит путь только в вершину Е. PГ(Л) = PЕ(Л) = 1.
Из вершины В выходят пути в вершины Д, Ж, Е и Г. Следовательно, PВ(Л) = PД(Л) + PЖ(Л) + PЕ(Л) + PГ(Л) = 1 + 0 + 1 + 1 = 3.
Из вершины Б выходят два пути в вершины Д и В.
PБ(Л) = PД(Л) + PВ(Л) = 1 + 3 = 4.
Из вершины А выходят два пути в вершины Б и Г.
PА(Л) = PБ(Л) + PГ(Л) = 4 + 1 = 5.
Получим:
| Л | К | Ж | Е | И | Д | Г | В | Б | А |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 | 3 | 4 | 5 |
Задача 3
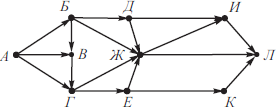
На рисунке изображена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Л, проходящих через пункт В?
Решение
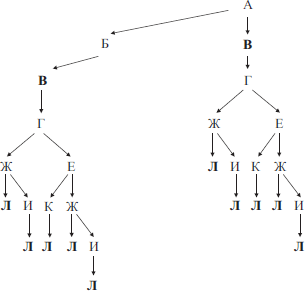
Построим граф, соответствующий данной схеме дорог. На графе будем для каждого города отмечать все возможные перемещения в города, связанные с ним исходящими дорогами.
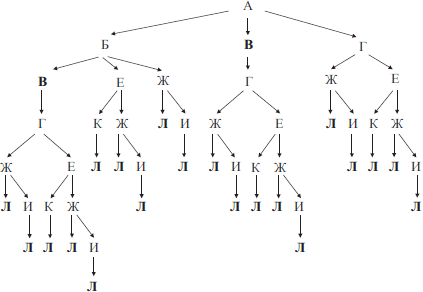
Согласно условию задачи, требуется определить количество путей, проходящих через город В.
По графу определяем, что существует всего 10 различных путей, проходящих через город В.
Задача 4
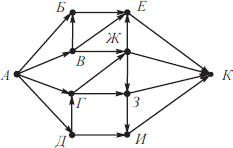
На рисунке изображена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?
Решение
Построим таблицу. В первую строку таблицы запишем наименование всех вершин в следующем порядке. Сначала запишем вершину К. Затем те вершины, из которых в К ведёт прямой путь и из которых в вершину К можно попасть только через уже просмотренные вершины. Далее вершины, из которых в уже просмотренные вершины ведёт прямой путь и из которых можно попасть только через уже просмотренные вершины. Получим:
| К | И | Е | З | Ж | Б | В | Г | Д | А |
Вторую строку таблицы заполним числами, соответствующими количеству исходящих путей Px(K) из просматриваемой вершины x в K. Если из вершины x выходит несколько путей, например, в вершины x1, x2, и x3, то количество путей, ведущих из этой вершины в К, будет равно сумме путей, ведущих из x1, x2, и x3 в К.
То есть Px(K) = Px1(K) + Px2(K) + Px3(K).
Например, из вершины Ж выходят пути в вершины Е, З и К. Следовательно, PЖ(K) = PЕ(K) + PЗ(K) + PК(K) = 1 + 2 + 1 = 4. Получим:
| К | И | Е | З | Ж | Б | В | Г | Д | А |
| 1 | 1 | 1 | 2 | 4 | 1 | 6 | 6 | 7 | ‘20 |
Задача 5
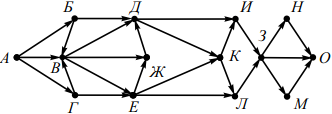
На рисунке изображена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М, Н, О. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город О, проходящих через город В?
Решение
Заметим, что количество путей из города А в город О, проходящих через город В равно произведению количества путей из города А в город В на количество путей из города В в город О. Разобъём заданный граф на два: один из которых будет содержать только города и соответствующие дороги, ведущие из А в В, а другой — только города и соответствующие дороги из В в О.
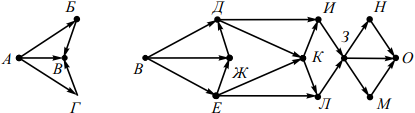
Построим таблицу, соответствующую каждой из полученных схем. В первую строку таблицы запишем наименование всех вершин в следующем порядке.
Для первой схемы сначала запишем вершину В. Затем те вершины, из которых в В ведёт прямой путь и из которых в вершину В можно попасть только через уже просмотренные вершины. Получим:
| В | Б | Г | А |
Вторую строку таблицы заполним числами, соответствующими количеству исходящих путей Px (B) из просматриваемой вершины x в B. Если из вершины x выходит несколько путей, например, в вершины x1, x2, и x3, то количество путей, ведущих из этой вершины в К, будет равно сумме путей, ведущих из x1, x2, и x3 в К.
То есть Px (B) = Px1 (B) + Px2 (B) + Px3 (B). Получим:
| В | Б | Г | А |
| 1 | 1 | 1 | 3 |
Количество путей из А в В равно 3.
Для определения количества путей из города В в О аналогично построим таблицу, соответствующую второй схеме.
| О | Н | М | З | И | Л | К | Д | Ж | Е | В |
| 1 | 1 | 1 | 3 | 3 | 3 | 6 | 9 | 9 | 18 | 36 |
Количество путей из В в О равно 36.
Следовательно, количество путей из города А в город О, проходящих через город В, равно 3 · 36 = 108.
Задача 6
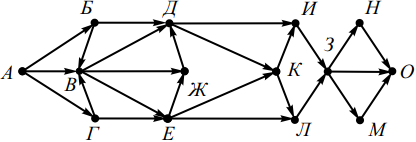
На рисунке изображена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М, Н, О. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город О?
Решение
Построим таблицу, соответствующую заданной схеме. В первую строку таблицы запишем наименование всех вершин в следующем порядке. Сначала запишем вершину О. Затем те вершины, из которых в О ведёт прямой путь и из которых в вершину О можно попасть только через уже просмотренные вершины. Далее вершины, из которых в уже просмотренные вершины ведёт прямой путь и из которых можно попасть только через уже просмотренные вершины. Получим:
| О | Н | М | З | И | Л | К | Д | Ж | Е | В | Б | Г | А |
Вторую строку таблицы заполним числами, соответствующими количеству исходящих путей Px (O) из просматриваемой вершины x в O. Если из вершины x выходит несколько путей, например, в вершины x1, x2, и x3, то количество путей, ведущих из этой вершины в К, будет равно сумме путей, ведущих из x1, x2, и x3 в К.
То есть Px (O) = Px1 (O) + Px2 (O) + Px3 (O). Получим:
| О | Н | М | З | И | Л | К | Д | Ж | Е | В | Б | Г | А |
| 1 | 1 | 1 | 3 | 3 | 3 | 6 | 9 | 9 | 18 | 36 | 45 | 54 | 135 |
Задача 7
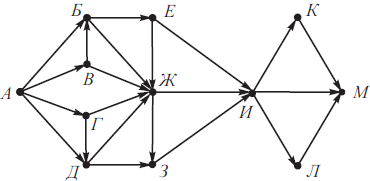
На рисунке изображена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город М?
Решение
Задача 8
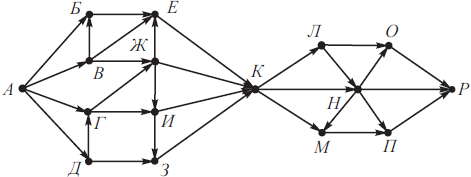
На рисунке изображена схема дорог, связывающих города А, Б, В, Г, Д, Е,Ж, З, И, К, Л, М, Н, О, П, Р. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей из города А в город Р, не проходящих через города Б и М?
Решение
Задача 9
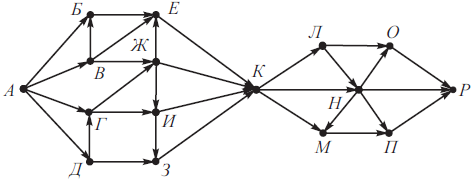
На рисунке изображена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М, Н, О, П, Р. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей из города А в город Р, не проходящих через города Е и Н?
Решение
Задача 10
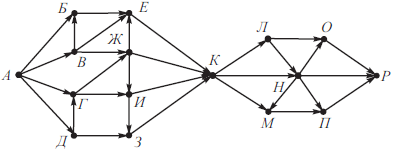
На рисунке изображена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М, Н, О, П, Р. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Р, проходящих через города З иМ?
Решение
Задача 11
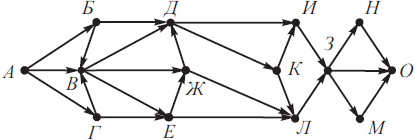
На рисунке изображена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М, Н, О. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город О, проходящих через город Е и не проходящих через город И?
Решение
Задача 12
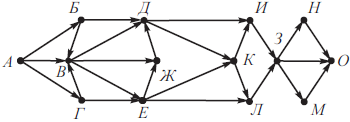
На рисунке изображена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М, Н, О. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город О, проходящих через город Д и не проходящих через город Л?
Решение
Задача 13
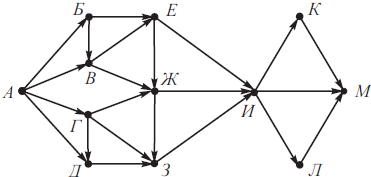
На рисунке изображена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город М, не проходящих через город В?
Решение
Задача 14
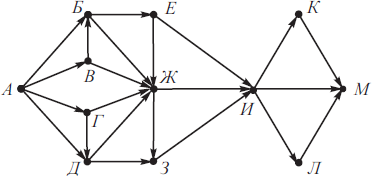
На рисунке изображена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город М, не проходящих через город Д?
Решение
Задача 15
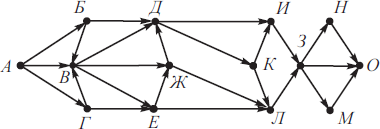
На рисунке изображена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М, Н, О. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город О, не проходящих через город Д?
Решение
Задача 16
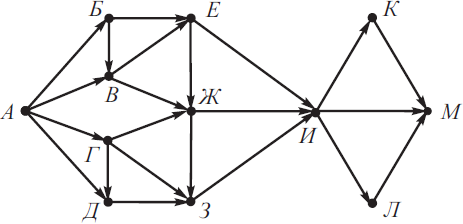
На рисунке изображена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город М, проходящих через город Е?
Решение
Задача 17
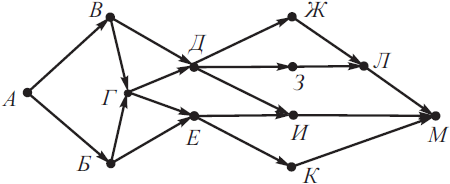
На рисунке изображена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город М, проходящих через город Б?
Решение
Задача 18
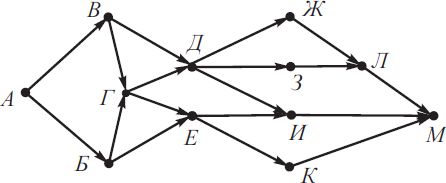
На рисунке изображена схема дорог, связывающих города А, Б, В, Г, Д, Е,Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город М, проходящих через город Д?
Решение
Задача 19
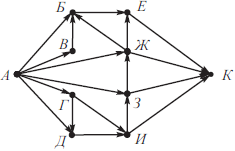
На рисунке изображена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?
Решение
Задача 20
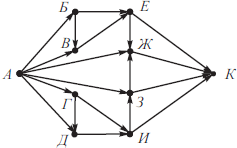
На рисунке изображена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?