Задание 2. Динамика. ЕГЭ 2024 по физике
Средний процент выполнения: 76.3%
Ответом к заданию 2 по физике может быть целое число или конечная десятичная дробь.
Задачи для практики
Задача 1
Пружину, жёсткость которой равна 1 · 104 Н/м, сжали с силой 400 Н. Вычислите потенциальную энергию, запасённую пружиной. Ответ выразите в (Дж).
Решение
Дано:
$k=10^4$Н/м
$F=400$Н
$E_{п}-?$
Решение:
Запишем закон Гука: $F=kx$(1), где $x$ — удлинение (в нашем случае, сжатие) пружины, $k$ — жесткость пружины. Откуда: $x={F}/{k}={400}/{10^4}=0.04$м.
Потенциальная энергия сжатой пружины определяется выражением: $E_{п}={kx^2}/{2}={10^4·16·10^{-4}}/{2}=8$Дж.
Задача 2
Точка финиша трассы горнолыжных соревнований находится на высоте 2 км над уровнем моря, а точка старта — на высоте 400 м над точкой финиша. Чему равна потенциальная энергия лыжника на старте относительно уровня моря? Масса лыжника 70 кг. Ответ выразите в (МДж).
Решение
Дано:
$m=70$кг
$g=10м/с^2$
$h_1=2000$м
$h_2=400$м
$E_{п}-?$
Решение:
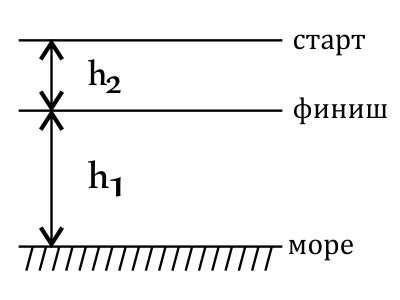
Потенциальная энергия лыжника на старте относительно уровня моря по определению равна: $E_{п}=mg(h_1+h_2)=70·10·(2000+400)=700·2400=1680000=1.68$МДж.
Задача 3
Тело массой 2 кг начинает свободно падать с высоты 5 м. Чему равна кинетическая энергия тела на высоте 2 м от земли? Ответ выразите в (Дж).
Решение
Дано:
$m=2$кг
$g=10м/с^2$
$h_1=5$м
$h_2=2$м
$E_{к_2}-?$
Решение:
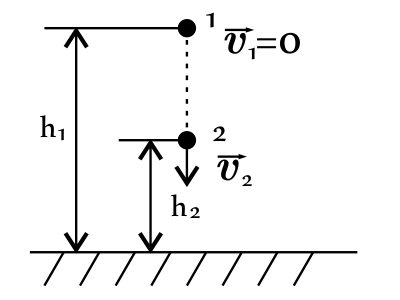
Полная механическая энергия тела в точке 1 равна полной механической энергии тела в точке 2: $E_1=E_2$(1), где $E_1=E_{п_1}+E_{к_1}=mgh_1+{mυ_1^2}/{2}=mgh_1$(2), $E_2=E_{п_2}+E_{к_2}=mgh_2+E_{к_2}$(3).
Подставим (2) и (3) в (1) и найдем $E_{к_2}:mgh_1=mgh_2+E_{к_2}$, откуда $E_{к_2}=mg(h_1-h_2)$(4).
Подставим числовые значения в (4), получим: $E_{к_2}=2·10·(5-2)=60$Дж.
Задача 4
Материальная точка массой 4,6 кг равномерно движется по окружности. Чему равна её скорость, если изменение её импульса за два с половиной периода составило 18,4 кг·м/с? Ответ выразить в (м/с).
Решение
Дано:
$m=4.6$кг
$t=2.5T$
$Δp↖{→}=18.4кгм/с$
$υ-?$
Решение:
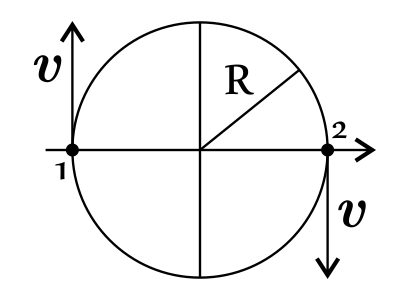 $Δp↖{→}={p_1}↖{→}-{p_2}↖{→}$
$Δp↖{→}={p_1}↖{→}-{p_2}↖{→}$
Исходя из рисунка $p_1$ и $p_2$ противонаправлены, тогда: $υ={Δp↖{→}}/{2·m}={18.4}/{2·4.6}=2м/с$
Задача 5
Падение тела массой 2 кг с некоторой высоты занимает 10 с. Найдите кинетическую энергию, которой будет обладать тело при падении на землю. Ответ выразите в (кДж).
Решение
Дано:
$m=2$кг
$t=10$с
$E_к-?$
Решение:
1) $E_к=E_n=mgh$ по закону сохранения
2) $S=H={gt^2}/{2}={10·100}/{2}=500$м
$E_n=mgh=2·10·500=10$кДж
Задача 6
Тело подбросили вертикально вверх с начальной скоростью 6 м/с. На какой высоте кинетическая энергия тела будет в два раза больше его потенциальной энергии? Ответ выразите в (м).
Решение
Дано:
$υ_0=6$м/с
$E_к=2·E_n$
$h-?$
Решение:
${table.{mυ_0^2}/{2}=E’_к+E’_n; .{E_к}/{2}=E_n;$
$⇒{mυ_0^2}/{2}=3E_n⇒{υ_0^2}/{2}=3gh$.
$h={υ_0^2}/{2g·3}={36}/{60}=0.6$м
Задача 7
На покоящуюся тележку массой 0,2 т налетает тележка массой 0,3 т со скоростью 8 км/ч . Найдите скорость, с которой эти тележки начали двигаться совместно после удара. Ответ выразите в (км/ч).
Решение
Дано:
$m_1=200$кг
$m_2=300$кг
$υ_1=8{км}/ч$
$υ_2-?$
Решение:
По закону сохранения энергии $m_1·0+m_2·υ_1=(m_1+m_2)υ_2$ выразим: $υ_2={m_2·υ_1}/{m_1+m_2}={300·8}/{200+300}=4.8{км}/ч$
Задача 8
Найдите, чему равно отношение масс большего тела к меньшему, если до абсолютного неупругого столкновения они двигались навстречу друг другу со скоростями 10 м/с каждое, а после — со скоростью 5 м/с.
Решение
Дано:
$υ_1=10м/с$
$υ_2=5м/с$
${M}/{m}-?$
Решение:
Запишем закон сохранения импульсов: $M·υ_1-m·υ_1=(M+m)υ_2$.
$10·M-10·m=5M+5m$
$5M=15m; {M}/{m}={15}/{5}=3$
Задача 9
Санки массой 50 кг из состояния покоя съезжают с гладкой наклонной плоскости высотой 5 м. После этого они продолжают двигаться по горизонтальной поверхности и спустя некоторое время останавливаются. Как при этом изменилась их механическая энергия? В ответе запишите: уменьшилась на _ (кДж).
Решение
Дано:
$m=50$кг
$h=5$м
$∆E_m-?$
$m_0=1·10^{-6}$кг
Решение:
По закону сохранения $∆E_m=∆E_h+∆E_к; ∆E_к=0$
$∆E_r=mgh=50·5·10=2.5$кДж. Тогда $∆E_{мех}=∆E_n=2.5$кДж.
Задача 10
Тела 1 и 2 взаимодействуют только друг с другом. Изменение кинетической энергии тела 1 за некоторый промежуток времени равно 15 Дж. Работа, которую совершили за этот же промежуток времени силы взаимодействия тел 1 и 2, равна 45 Дж. Чему равно изменение кинетической энергии тела 2 за это время? Ответ выразить в (Дж).
Решение
Дано:
$∆E_1=15$Дж
$∆E_в=45$Дж
$∆E_2-?$
Решение:
По закону сохранения энергии запишем уравнение взаимодействия: $∆E_1+∆E_2=∆E_в⇒∆E_2=∆E_в-∆E_1$
$∆E_2=45-15=30$Дж
Задача 11
Мальчик столкнул санки массой 2 кг с вершины горки. Сразу после толчка санки имели скорость 4 м/с, а у подножия горки она равнялась 8 м/с. Трение санок о снег пренебрежимо мало. Какова высота горки? Ответ выразите в (м).
Решение
Дано:
$υ_0=4$м/с
$υ_к=8$м/с
$F_{тр}=0$
$H-?$
Решение:
Запишем закон сохранения энергии для данного случая $E_{к_0}+E_п=E_к^к$. $E_{к_0}$ — кинетическая энергия в начальный момент; $E_п$ — потенциальная энергия в начальный момент; $E_к^к$ — кинетическая энергия в конце пути.
$E_п=E_к^к-E_{к_0}$
$mgH={m·υ_к^2}/{2}-{m·υ_0^2}/{2}$
$2·10·H=64-16⇒H=2.4$м
Задача 12
Легковой автомобиль и грузовик движутся со скоростями 108 км/ч и 72 км/ч соответственно. Масса грузовика 4500 кг. Какова масса легкового автомобиля, если импульс грузовика больше импульса легкового автомобиля в 2 раза? Ответ выразите в (кг).
Решение
Дано:
$υ_л=108$км/ч$=30м/с$
$υ_г=72$км/ч$=20м/с$
$m_г=4500кг$
$p_г=2p_л$
$m_л-?$
Решение:
По определению импульс тела равен: $p=mυ$(1), тогда $p_г=m_г·υ_г$(2) — импульс грузового автомобиля; $p_л=m_л·υ_л$(2) — импульс легкового автомобиля. По условию задачи: $p_г=2p_л$(4). Подставим (2) и (3) в (4): $m_г·υ_г=2m_лυ_л⇒m_л={m_г·υ_г}/{2υ_л}$(5). Подставим числовые значения в (5): $m_л={4500·20}/{30·2}=1500кг$.
Задача 13
Ученик исследовал зависимость силы упругости F пружины от её растяжения x и получил следующие результаты:
| F, H | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 |
| x, см | 0 | 2 | 4 | 6 | 8 | 10 |
По данным опыта определите, какую работу нужно совершить, чтобы растянуть пружину от 4 см до 8 см. Ответ выразите в (Дж).
Решение
Дано:
$x_1=4см=4·10^{-2}м$
$x_2=8см=8·10^{-2}м$
$A-?$
Решение:
Работа силы упругости пружины равна убыли ее потенциальной энергии: $A={kx_1^2}/{2}-{kx_2^2}/{2}$(1), где $k$ — жесткость пружины.
Найдем жесткость пружины $k$. Для этого возьмем любые значения силы упругости пружины и растяжения, отличные от нуля, например, $F_{тр}=1H, x=0.04м$. Тогда, по закону Гука имеем: $F_{упр}=kx⇒k={F_{упр}}/{х}$(2). $k={1}/{0.04}=25Н/м$
Подставим числовые значения в (1) и найдем работу $A$: $A={25}/{2}((4·10^{-2})^2-(8·10^{-2})^2)=12.5·(16·10^{-4}-64·10^{-4})=-600·10^{-4}=-0.06$Дж.
Зная, что «минус» говорит о том, что при растяжении сила упругости направлена противоположно растяжению пружины.
Задача 14
Шарик массой 100 г налетает со скоростью 2 м/с на покоящийся шар такой же массы. Каков импульс системы шаров после абсолютно неупругого удара? Ответ выразите в (кг·м/с).
Решение
Дано:
$m_1=m_2=m=0.1кг$
$υ_1=2{м}/{с}; υ_2=0{м}/{с}$
$p-?$
Решение:
По закону сохранения импульса: импульс системы до взаимодействия равен импульсу системы после взаимодействия: $p=p_1+p_2=m_1·υ_1+m_2·υ_2=m_1υ_1=0.1·2=0.2{кг·м}/{с}$
Задача 15
Кинетическая энергия равномерно движущегося тела массой 200 г равна 10 Дж. С какой скоростью движется тело? Ответ выразите в (м/с).
Решение
Дано:
$m=200г=0.2кг$
$Е_к=10Дж$
$υ-?$
Решение:
Кинетическая энергия определяется выражением:$Е_к={mυ^2}/{2}$(1), откуда выразим скорость $υ: $.
Учитывая, что $mυ^2=2Е_к$, $υ^2={2E_к}/{m}$, $υ=√{{2E_к}/{m}}$(2).
Подставим числовые значения в (2): $υ^2=√{{2·10}/{0.2}}=√{100}=10{м}/{с}$
Задача 16
Тело массой 200 г, двигаясь равномерно, обладает импульсом 4 кг·м/с. Какова его кинетическая энергия? Ответ выразите в (Дж).
Решение
Дано:
$m=200г=0.2кг$
$p=4{кг·м}/{с}$
$Е_к-?$
Решение:
Импульс по определению равен: $p=mυ$(1), а кинетическая энергия определяется выражением:$Е_к={mυ^2}/{2}$(2).
Учитывая, что $mυ^2={m^2υ^2}/{m}={(mυ)^2}/{m}={p^2}/{m}$(3), подставим (3) в (2): $Е_к={p^2}/{2m}$(4).
Подставим числовые значения в (4): $Е_к={4^2}/{2·0.2}={16}/{0.4}=40$Дж